בנפתולי המחשב: משחק הקלפים של הקבצים
בקליק אחד אתם מסדרים את אלפי הקבצים והתיקיות במחשב לפי סדר. מאחורי הקלעים, המחשב צריך לעבוד ולמיין את הכל נורא מהר. קחו קלפים והתחילו להתאמן
כמו לכולם, גם לכם יש לפחות תיקייה אחת שמכילה מאות ואולי אלפי קבצים של תמונות. לפעמים בא לכם שהמחשב יסדר אותם לפי סדר כרונולוגי ולפעמים לפי השם שלהם. חשבתם פעם איך עושים כזה סידור כמה שיותר מהר ויעיל? גם לא - תחשבו עכשיו.
- בשבוע שעבר למדנו איך הכונן הקשיח (לפחות בחלק ממערכות ההפעלה) מסדר את הקבצים כדי לגשת אליהם אחר כך, והמלצנו לא לגזור חולצות.
כמו למיין קלפים
בואו נניח שנחטפתם על ידי שודדים שאוהבים מתמטיקה. זה לא קורה הרבה, אבל זה עוזר להסביר איך המיון הזה עובד. השודדים נותנים לכם את האופציה להשתחרר, אם תצליחו לבצע שתי משימות: במשימה הראשונה הם נותנים לכם חבילה של 10 קלפים, שכל קלף יכול להכיל מספר שונה מ 1 עד 2,000. אתם צריכים לסדר אותם לפי סדר עולה כשלרשותכם עומדות חמש דקות בלבד.
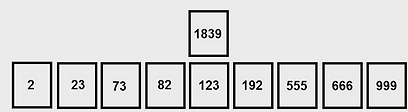
השיטה שאתם בוחרים היא כזו לעבור על כל החבילה, למצוא את הקלף עם המספר הכי קטן, לשים אותו ראשון בצד, וכך שוב ושוב עם יתר הקלפים עד שסידרתם הכל בערימה. בחבילה שלנו, בפעם הראשונה צריך לעבור על 10 קלפים והקלף עם המספר 2 הוא הכי קטן.
כעת נותרו 9 קלפים עליהם יש לעבור, והקלף עם המספר 23 הוא הכי קטן.
כך אתם ממשיכים עד שנשארתם עם קלף אחד, שמצוין עליו את המספר הכי גבוה, ואותו שמים אחרון בחבילה החדשה.
לצורך דיוננו בואו נניח שהשוואה בין שני קלפים, והנחת קלף בסוף החבילה החדשה לוקחים לכם חצי שניה. בשיטה הזאת ייקח לכם השלב הראשון 10 חצאי שניות (5 שניות), השלב השני ייקח 4.5 שניות וכל התהליך ייקח 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 חצאי שניות, שהם 27.5 שניות. הרבה פחות מחמש הדקות שהקצו לכם החוטפים. יש! אתם בדרך הנכונה.
אבל מה עושים כשיש מלא קלפים?
במשימה השנייה נותנים לכם החוטפים חבילה של 1000 קלפים ומקציבים לכם יום שלם, 24 שעות, לסדר אותם לפי סדר עולה. לפני שאתם מתחילים אתם בודקים כמה זמן זה ייקח לכם ומגלים לתדהמתכם ש 1000 + 999 + .... + 3 + 2 + 1 חצאי שניות הם כמעט 3 ימים רצופים. אם תנסו לסדר בשיטה זאת לא רק תכשלו קשות, אלא גם תשתגעו, וגם קרוביכם יאלצו לשלם כופר גבוה עבור השחרור שלכם (בהנחה שלקרוביכם אכפת מכם).
באופן כללי המאמץ לבצע את המשימה (או כמו שקוראים לזה במדעי המחשב "הסיבוכיות של המשימה"), היא כמספר הקלפים בריבוע (בחזקת 2). שיטה זו פשוטה להבנה אך מאד יקרה לביצוע, ובמדעי המחשב לא משתמשים במושג שיטה אלא במושג אלגוריתם.
לטייל על העץ
לאלגוריתם הזה קוראים Bubble Sort (מיון בועות) כי הוא "מציף" למעלה כל פעם את הקלף הכי קטן. אתם יכולים גם להסיק, שאפילו אם את הסידור היה עושה מחשב שמסוגל לעשות זאת פי כמה וכמה יותר מהר מבני האדם, סידור של 1,000,000 קלפים עדיין יעסיק אותו לזמן רב, ואתם תישארו בשבי.
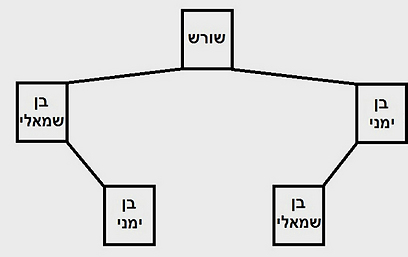
כדי לעזור לכם - או.קיי, לא רק לכם, גם לשאר העולם - להיות יותר יעילים בסידורים, פיתחו מדעני המחשב צורת אחסון שמבוססת על "עץ בינארי". עץ בינארי נראה הפוך מעץ רגיל. למעלה השורש ומכל ענף (שנקרא גם צומת) יכולים להתפצל עד שני ענפים נוספים שנקראים הבן השמאלי והבן הימני.
אנחנו נשתמש בעץ הבינארי בצורה כזאת, שמספר שנמצא בבן הימני הוא יותר גדול מענף שמעליו (שנקרא האבא שלו) ומספר שנמצא בבן השמאלי יותר קטן מהאבא שלו. האלגוריתם שנשתמש בו יהיה כדלקמן: קחו מספר מהחפיסה ותתחילו לטייל בעץ מהשורש. אם המספר שבידכם יותר גדול ממה שיש בענף לכו ימינה. אחרת - לכו שמאלה. אם הגעתם למקום ריק בעץ שימו את המספר.
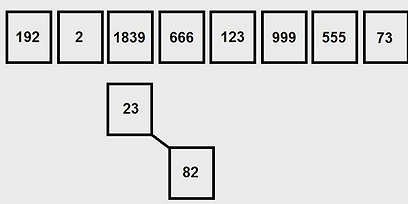
כך ייראה העץ אחרי שהכנסנו את שני המספרים הראשונים מהחפיסה, 23 ו 82.
כך ייראה העץ אחרי שהכנסנו את שני המספרים הבאים, 192 ו 2.
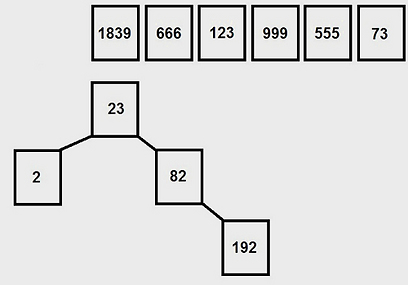
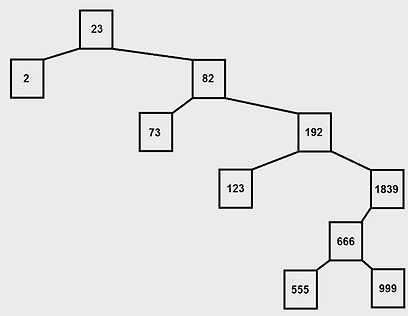
וכך ייראה העץ אחרי שהכנסנו את כל המספרים.
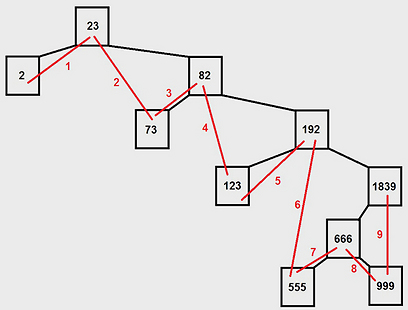
מה שנשאר עכשיו לעשות זה ל"טייל" על העץ, מהבן הכי קטן (שהוא הבן הכי שמאלי בעץ), בשיטה של הבן הכי שמאלי-אבא-בן ימין וכולי. אם נעקוב אחרי הטיול הזה, נראה שהתוצאה שלו היא 2,23,73,82,123,192,555,666,999,1839 וזה מה שרצינו שיצא לנו.
יותר מהר?
אין ספק שהאלגוריתם הזה יותר מסובך מהקודם, ודורש הרבה יותר מקום על רצפת החדר שבו אתם מוחזקים בשבי, אבל האם הוא יותר יעיל? האם הוא יעזור לכם להיחלץ מהשבי?
דבר ראשון צריך לבדוק "כמה עולה" להכניס מספר לעץ הבינארי. התשובה היא שזה תלוי איך העץ נראה, וכמה צמתים יש בו. בממוצע, ולא נסביר זאת פה לעומק, זה עולה log2(n). כאשר n הוא מספר הצמתים (המספרים) שכבר הכנסנו לעץ. רק כדי לסבר את האוזן עבור 100 צמצים מדובר ב-9.97 ועבור מיליון צמתים מדובר ב-19.93 צעדים.
לכן, עלות ההכנסה במקרה של 1,000 מספרים היא 1,000 * Log2(1,000) = 9970 צעדים. עלות "הטיול" בעץ זה פשוט. מספר המספרים שהכנסנו - ובמקרה שלנו זה 1,000. אם כל פעולה לוקחת חצי שניה, (9970 + 1000) X חצי שניה = 5,485 שניות, או שעה וחצי. יש! החוטפים ישחררו אותנו.
בטבלה הזאת אפשר לראות את ההשוואה בין שני האלגוריתמים, כששוב ההנחה היא שכל פעולה לוקחת חצי שניה, ואסור לעשות הפסקות קפה.

יש עוד שיטות סידור ומיון רבות וכמו גם צורות אחסון (הנקראות מבני נתונים). לכל אחת מהן יתרונות וחסרונות, וכל אחת מתאימה לסוג שונה של בעיות (זוכרים את סידור קבצי התמונות במחשב?). מומלץ ללמוד אותם, כי לכו תדעו מה ירצו החוטפים המתמטיים בפעם הבאה.
- כשניר כץ לא ממיין קלפים הוא כותב בלוג בשם החיים על פי ניר