הנמלה והחלקיק: המסתורין של 0.577
הוא התגלה לפני כמעט 300 שנה, אבל עדיין לא יודעים אם הוא רציונלי. הוא מופיע במשוואות רבות, אבל נותר אלמוני ביחס לפאי. הכירו את קבוע אוילר, וצפו בסרטון החדש שכבש את הרשת
לשאלה מהו המספר המפורסם בעולם יש כנראה תשובה אחת ברורה - פאי. אבל המספר שקירובו הוא 3.14 ומופיע כמעט בכל מקום בטבע ובמתמטיקה הוא לא היחיד בעל תכונות מיוחדות. מספר נוסף שכזה, ידוע הרבה פחות, הוא 0.577, בערך. בסרטון של "נמברפיל" שהביא את סיפורו ופורסם בשבוע האחרון כבר צפו יותר מרבע מיליון איש, ועכשיו גם אתם תוכלו להכיר אותו.
המספר המוכר כקבוע אוילר, או קבוע אוילר-מסקרוני, מוגדר על ידי ההפרש האסימפטוטי בין שני רצפים מתמטיים קלאסיים - הסדרה ההרמונית והלוגריתם הטבעי. הסדרה ההרמונית, או במילים אחרות הטור ההרמוני, היא סדרה מפורסמת שסיכום מספריה שואף לאינסוף. תחילתה - 1+1/2+1/3+1/4 וכך הלאה. הלוגריתם הטבעי, שבסיסו הוא המספר המפורסם הנוסף e (וקירובו 2.718), קשה יותר להסבר.
בכל מקרה, תוצאת ההפרש בין הטור ההרמוני לבין הלוגריתם הטבעי שואפת לאותו קבוע אוילר. כמו פאי, גם את קבוע אוילר אפשר להמשיך הרבה מעבר לשלוש הספרות הראשונות שאחרי הנקודה - למעשה, בערך ל-100 מיליארד מספרים אחרי ה-0.577.
הסרטון המלא
בסרטון ניתן לראות דוגמה לאותה סדרה הרמונית. למשל, דמיינו שיש לכם מעגל שהיקפו מטר אחד, ואתם מציבים נמלה בראשו. אותו נמלה מתחילה לנוע בקצב קבוע של ס"מ בשנייה. אבל בזמן שהנמלה זזה לה, היקף המעגל מורחב במטר בכל שנייה. אז, למעשה, בכל שנייה הנמלה מתקדמת בסנטימטר אחד במעגל - אבל היקפו גדל במטר. אז אין סיכוי שהיא תסיים את מסעה במעגל, נכון?
התשובה, למרבה התדהמה, היא לא. הנמלה יכולה לסיים את מסעה במעגל אם היא צועדת בקצב קבוע, והסיבה לכך היא שלא רק המרחק שנותר שלה גדל, אלא גם המרחק שמאחוריה. עם זאת, ברור שמדובר במסע תיאורטי בלבד - לנמלה ייקח זמן עצום להשלים את מסעה - הרבה יותר ממיליארדי מיליארדים של שנים.
קבוע אוילר עצמו נמצא בתחומים רבים בפיזיקה, ובכלל זאת במשוואות של מכניקת הקוונטים ובכאלה שנועדו לאיתור "החלקיק האלוהי", בוזון היגס. אם אתם לא מסתפקים בשלוש הספרות הראשונות, נאמר לכם שקירובו המדויק של קבוע אוילר הוא 0.5772156642901532850. ולמרות שהוא הוגדר לראשונה על ידי המתמטיקאי השוויצרי לאונרד אוילר כבר ב-1761 – עדיין לא ברור אם זהו מספר רציונלי או אי-רציונלי.
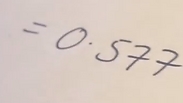
0.577
מומלצים








