כדי לתכנן חניון רב-קומות, תחילה יש להבין מהי כמות המכוניות המירבית שאפשר לדחוס לחלל קטן ככל האפשר, תוך הבטחת תנועה חופשית בין הקומות השונות. למבנים דמויי-חניונים בתאי צמחים ובעלי-חיים יש תפקיד דומה: הם בנויים כשכבות דקות ושטוחות, המחוברות באמצעות "רמפות" סליליות, אשר מאפשרות תנועה חופשית של מולקולות והעברתם של חומרים שונים. בתאי בני-אדם, לדוגמה, מבנים אלה מסייעים בתנועה הנדרשת להפקת חלבונים ולקיפולם. בתאי צמחים, הם מאחסנים את החומרים הנחוצים עבור פוטוסינתזה.
הרמפות בחניונים יצוקות בבטון וקבועות במקום. אך מפני שחניונים ביולוגיים מורכבים מקרומים רכים, הרמפות שנוצרות מסוגלות לנוע, ולמקם את עצמן מחדש בהתאם לצורך. כוחות עדינים קובעים את תנועת הרמפות הביולוגיות, אבל כדי להבין את הכוחות האלה, ראשית יש לפענח את המבנה הגיאומטרי שלהן. במחקר חדש שהתפרסם באחרונה, ד"ר אפי אפרתי ותלמיד המחקר הבתר-דוקטוריאלי ד"ר לואיז דה סילבה, מהמחלקה לפיזיקה של מערכות מורכבות במכון ויצמן למדע, גילו שלא קיימים כלים מתמטיים מתאימים לתיאור התופעה – ולכן, פיתחו בעצמם כלים חדשים.
2 צפייה בגלריה


מימין: ד״ר לואיז דה סילבה וד״ר אפי אפרתי. מעט המחזיק את המרובה
(צילום: מסע הקסם המדעי, מכון ויצמן למדע)
ד"ר אפרתי משתף פעולה כבר מספר שנים עם פרופ' זיו רייך, מהמחלקה למדעים ביומולקולריים, במחקר שעוסק במבנים דמויי-חניון הקרויים תילקואידים. במבנים אלה, המצויים בתאי צמחים ובתאי אצות ירוקות, מתבצע חלק מתהליך הפוטוסיתנזה. המבנה של התילקואידים מאפשר להם לדחוס הרבה שטח פנים לחלל קטן.
שיחזור של מבנה התילקואידים, שאותו ביצעה קבוצת המחקר של פרופ' רייך באמצעות מיקרוסקופ אלקטרונים, הראה שהתילקואידים מתארגנים לכדי משטחים מינימליים - משטחים אשר נוצרים במערכות ביולוגיות, וקיימים גם במבנים מלאכותיים, המשתרעים על פני המרחב הקטן ביותר במסגרת גבול נתון. המדענים אף גילו שהרמפות במבנים אלה מסוגלות להתעקל שמאלה או ימינה, בשיפועים שונים. הכלים הפיסיקליים הקיימים איפשרו לתאר את את שיפוע המדרון, אבל כדי להבין את האופן שבו מתמקמים המבנים השונים במרחב, ומה קובע את היחס בין המדרון לקוטר הרמפה, היו חייבים המדענים לפתח כלים חדשים – מדויקים יותר.
משטחים מינימליים התגלו לראשונה במאה ה-18 והם, ככל הנראה, סוג המשטח הנחקר ביותר בעולם המתמטיקה. הדרך הטובה ביותר לסדר משטח מינימלי באמצעות רמפה סלילית, לדוגמה, ידועה כבר 250 שנה. יחד עם זאת, בניית משטח מינימלי שמזכיר את הצורה הגיאומטרית המפותלת של תילקואיד היא סיפור אחר לחלוטין. "כפיסיקאים, יש לנו נטייה להשתמש בקירובים", אומר ד"ר אפרתי. "התחלנו עם עיצוב מערכת שהתבססה על קירוב מתמטי נפוץ לחישוב משטחים מינימליים". הקירוב איפשר להם להניח מוטיבים סליליים באופן שרירותי ולבנות "חניונים" גיאומטריים מורכבים, אבל המבנים שנוצרו לא נפלו תחת ההגדרה של משטחים מינימליים. "גילינו שהקירובים מתאימים רק כאשר המבנים רחוקים זה מזה".
2 צפייה בגלריה
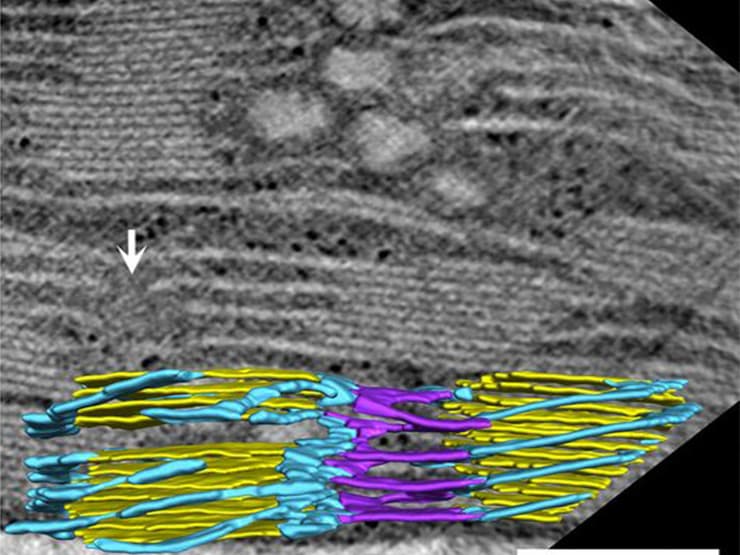

מודל תלת-ממדי של רשת קרומים פוטוסינתטיים בצמח, המבוסס על צילומי מיקרוסקופ אלקטרונים. תילקואידים (בצהוב) מוקפים במבנים דמויי-חניון, המורכבים מרמפות המעוקלות שמאלה (בסגול) וימינה (בכחול)
(צילום: מסע הקסם המדעי, מכון ויצמן למדע)
במקום להתחיל מההתחלה, ד"ר דה סילבה וד"ר אפרתי ניסו למצוא דרך לתקן את הקירוב. "התוצאה נראתה כפי שרצינו, אבל עם הבדלים דקים, אז השתמשנו בה כנקודת פתיחה עבור החישובים שביצענו". לבסוף מצאו המדענים את הפתרון: תימרון שמביא בחשבון את הקירוב של כל המשטח והרמפות הסליליות שלו, ואז מחשב בנפרד את עקמומיותה של כל נקודה ונקודה על-גבי המשטח. התוצאה שהתקבלה היתה משטח מינימלי מדויק עם המבנים הסליליים הרצויים מוטבעים בתוכו.
מעבר לכך שהמודל שפיתחו ד"ר אפרתי וד"ר דה סילבה מאפשר בנייה מדויקת של משטח מינימלי בעל מאפיינים גיאומטריים מורכבים, הוא אף יאפשר לביולוגים לבצע ניתוח כמותי של אברוני תא. כיוון שמבנים דמויי-חניונים מסוג זה מצויים במערכות ביולוגיות רבות, המחקר החדש מאפשר להבין טוב יותר את המבנה של אברונים חשובים בתאים כמו התילקואיד, ואולי אף יאפשר לעצב מבנים מיקרוסקופיים סינתטיים בעלי מאפיינים דומים.
הכתבה פורסמה לראשונה ב"מסע הקסם המדעי", מכון ויצמן למדע

