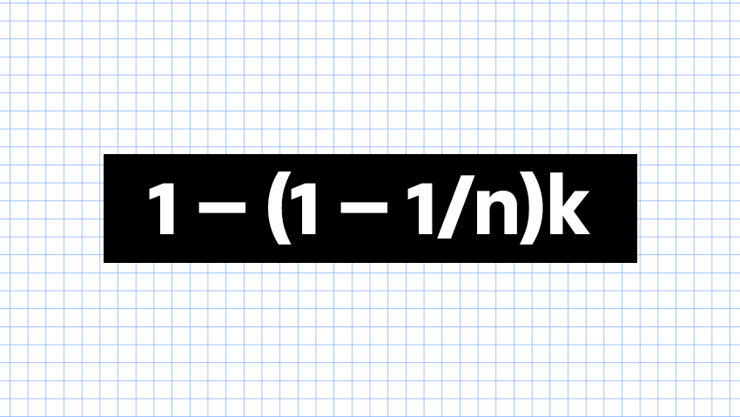לא מזמן עברתי חוויה מוזרה בבית קפה. לאחר ששילמתי על הקפה, ביקשתי להשתמש בשירותים. בזמן שהקשתי את קוד כרטיס האשראי שלי בקורא האשראי, הושיט לי הבריסטה פתק ועליו מספר. היה זה אותו המספר שבדיוק הקשתי במכשיר! התברר שזה גם קוד הכניסה לשירותים.
- לא רוצים לפספס אף כתבה? הצטרפו לערוץ הטלגרם שלנו
עוד כתבות למנויים:
האם נפלתי קורבן למזימה מפוקפקת של סוכני קפאין? לא, הייתה זו מקריות בלבד, אבל האירוע גרם לי לחשוב על צירופי מקרים באופן כללי. לפרקים קורה לנו שאנו חווים אירועים שנראים כל כך בלתי סבירים, עד שקשה שלא להרגיש שהיקום שולח לנו מסר. אולם כמתמטיקאית, אני יודעת שהסיכוי של צירופי מקרים להתרחש הוא הרבה יותר גבוה ממה שאנו נוטים לחשוב, ויש לעובדה הזו השלכות משמעותיות בכל תחום, החל ממעבדות מחקר, דרך קיוסקים של לוטו ועד לבתי המשפט.
חווית בית הקפה שלי היא מקום טוב להתחיל בו, משום שאפשר לחשב את ההסתברות המדויקת של מקריות האירוע. למספרים בני ארבע ספרות יש 10,000 צירופים אפשריים, כלומר יש הסתברות של 1 ל-10,000 שקוד הדלת יהיה תואם לקוד כרטיס האשראי שלי. זהו סיכוי נמוך, נכון, אבל הבה נשים אותו בתוך הקשר. בית הקפה היה בעיר יורק שבבריטניה - יעד תיירותי פופולרי, עם 8.9 מיליון מבקרים בשנה. בהנחה שלכל מבקר יש כרטיס אשראי אחד לפחות, ניתן לצפות שמדי שנה יהיו כ-890 כרטיסים עם קוד הזהה לקוד הכניסה לשירותי בית הקפה. אני מרגישה קצת פחות מיוחדת עכשיו.
צירוף המקרים בבית הקפה ממחיש לנו עובדה חשובה: אפילו אירועים מאוד לא סבירים עשויים להתרחש, אם רק יתקיימו מספיק הזדמנויות. נוכל לבטא זאת באופן מתמטי בצורה הבאה: כאשר לאירוע יש k הזדמנויות להתרחש, וכאשר לכל הזדמנות יש סיכוי של אחד ל-n להתרחש, אזי (בהנחה שהאירועים הם בלתי תלויים) ההסתברות שהאירוע יתרחש לפחות פעם אחת היא:
אל תתנו לאלגברה להרתיע אתכם: המסר שאפשר לקחת מכאן הוא שהסיכוי לצירוף מקרים עולה מאוד ככל שמספר ההזדמנויות גדל. מהנוסחה עולה המסקנה הבאה: ההסתברות שאירוע עם סיכוי של "אחד ל-n" להתרחש לפחות פעם אחת, תחצה את רף ה-50% בכל פעם שיש יותר מ- 0.7n הזדמנויות בלתי תלויות להתרחשותו. את התופעה הזו אני מכנה בשם "כלל 0.7".
נמחיש זאת בכמה דוגמאות. נניח שבברמינגהם, לכל תושב יש סיכוי של אחד למיליון לחלום בלילה את החדשות של מחר. מכיוון שהאוכלוסייה מונה למעלה מ-700,000 איש, סביר להניח שבכל יום יש מישהו בברמינגהם שקם בבוקר ומשוכנע שהוא רואה עתידות.
מדי יום יש שלל דרכים שעשויות לזמן לכם צירוף מקרים חריג. נניח שההזדמנות שלכם לחוות צירוף מקרים חריג היא פעם בשעה. בהנחה שתוחלת החיים החציונית היא 706,000 שעות, יש סיכוי טוב שתחוו צירוף מקרים חריג (של אחד למיליון) לפחות פעם אחת במהלך חייכם.
ניתוחים כאלה מסייעים להסביר כמה מצירופי המקרים המדהימים ביותר בהיסטוריה, כמו המקרה יוצא הדופן של הלוטו הלאומי בבולגריה, אשר בספטמבר 2009, יצאו בו אותם המספרים ( 4, 15, 23, 24, 35 ו-42 ) בשתי הגרלות רצופות.
המקרה נשמע כמו רמאות, אבל הסטטיסטיקאי דייוויד הנד חישב ומצא שנדרשות 43 שנים של הגרלות לוטו כדי להגיע למצב שבו הסבירות שאותם המספרים יוגרלו לפחות פעמיים, תעלה על הסבירות שזה לא יקרה (במועד התרחשות האירוע, ההגרלה רצה כבר 52 שנים).
לכל כרטיס לוטו יש סיכוי שווה לזכות, אבל אנשים הם לא כרטיסי לוטו, ולכן ההסתברות לחוות אירוע נדיר משתנה מאדם לאדם. רוי סאליבן, מפקח פארקים מווירג'יניה, נפגע מברק שבע פעמים בין השנים 1942 ל-1977. מדובר ללא ספק בחוסר מזל, אבל לרוי היה סיכוי גבוה יותר להיפגע מברק מאשר לרוב האנשים. באזורים החמים והלחים יותר של ארה"ב יש יותר ברקים, ואנשים שעובדים במקום פתוח חשופים יותר מאלה שעובדים מוגנים בתוך מבנים. העבודה במקום פתוח גם עוזרת להסביר, ולו חלקית, מדוע 84% ממקרי המוות כתוצאה ממכת ברק הם של גברים.
קורה גם שההסתברות נראית מרשימה מכפי שהיא באמת. התחזית של ה"מדיום" המפורסמת, ג'ין דיקסון, לפיה ג'ון פ. קנדי ינצח בבחירות לנשיאות של 1960 וימות במהלך כהונתו נראתה נבואית להדהים, עד שמגלים שהיא גם חזתה ניצחון של ניקסון ב-1960 ואת תחילתה של מלחמת עולם שלישית ב-1958. זה בסדר, ג'ין. במילותיו המפורסמות של נילס בוהר - קשה מאוד לנבא, במיוחד את העתיד.
כמובן שלפעמים יש סיבה למקריות. אם אדוארד ג'נר היה מתעלם מהמקריות המוזרה שנשים חולבות הראו חסינות יוצאת דופן לאבעבועות שחורות, ייתכן שלעולם לא היה מגלה שהן מוגנות מהמחלה הודות לחשיפה קודמת שלהן ל"אבעבועות הבקר", גילוי שהוביל לחיסון המוצלח הראשון בעולם.
ההבחנה בין צירופי מקרים לבין מקריות שיש לה סיבה היא מיסודות השיטה המדעית, ויש לה שימוש גם בפיצוח מקרים של חשד להעתקות. "Shape of You", הלהיט של אד שירן שהגיע לראש המצעדים, הוא דוגמה טובה. השיר עמד במרכזה של תביעה משנת 2022, שטענה כי רצף של ארבעה תווים מתוכו הועתק משיר משנת 2015 בשם "Oh Why?", של סמי צ'וקרי.
"כאשר 60,000 שירים מתווספים מדי יום לספוטיפיי, צירוף מקרים הוא רק עניין של זמן", אמר שירן למעריציו לאחר שזכה בתביעה. "יש 22 מיליון שירים חדשים בשנה ורק 12 תווים".
הוא צודק – באוקטבה המערבית יש 12 תווים, ולכן מספר הצירופים האפשריים לארבעה תווים הוא 20,736 בלבד. ניתן לומר בוודאות מתמטית כי רבים מאותם 22 מיליון שירים שיוצאים מדי שנה יכילו קטעים דומים להפליא.
באקדמיה, היכולת להבחין בין דמיון מקרי לבין העתקה או שימוש אסור בבינה מלאכותית לשם כתיבת עבודות סטודנטים, היא אתגר גובר. Turnitin הוא כלי לזיהוי העתקות, אולם יש לו סיכוי של 1% לשגות בזיהוי, ולסמן עבודה כמכילה מעל 20% תוכן בינה מלאכותית. ומה אם נפלתם בתוך האחוז הבודד הזה? כיצד תוכיחו שלא רימיתם? לואיז סטיברס, סטודנטית מאוניברסיטת קליפורניה, הצליחה לשכנע את האוניברסיטה בחפותה רק לאחר שהציגה טיוטות מעבודתה שכללו חותמת זמן.

בימים אלה של סוף השנה האזרחית אנו מרבים למצוא את עצמנו במסיבות, מפטפטים עם אנשים שאנו לא מכירים בניסיון לאתר נושאים משותפים. למרבה השמחה, חיבורים כאלה יימצאו כמעט בוודאות. ההערכה היא שכל אחד מאתנו מכיר כ-1000 אנשים (מכרים, קולגות, שכנים - נקרא לכולם "חברים" לשם קיצור). בהנחה שהקשרים בין כולם מתפלגים באופן אקראי, יש סיכוי של יותר מ-99% שלכם ולי יש חבר משותף, או חבר שמכיר את אחד החברים שלי.
אולם בחיים האמיתיים, הרשתות החברתיות רחוקות מלהראות התפלגות אקראית. למשל, סביר יותר שתכירו מישהו מעיר מגוריכם מאשר ממקום אחר. אלא שבאופן מפתיע, אין לכך השפעה רבה על האפקטים של המקריות.
המתמטיקאים סטיבן סְטְרוֹגַץ ודנקן ווטס גילו שדי בנוכחותם של כמה אנשים עתירי חברים כדי להביא את ההתפלגות של כלל הקשרים להיות קרובה להתפלגות אקראית. המשמעות היא שגם אם לרובנו יש רק 100 חברים בממוצע, כל שני אנשים ימצאו שהם מחוברים ביניהם בשרשרת שאורכה חמישה חברים בלבד.
שיחות חולין בין אנשים זרים מכונות small talk, וכנראה בצדק: זה באמת עולם קטן. הודות לחוקי המתמטיקה צירופי המקרים הם רבים, ואירועים שנראים כיד הגורל הם לרוב לא יותר ממשחק של מספרים.