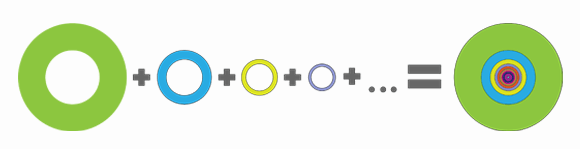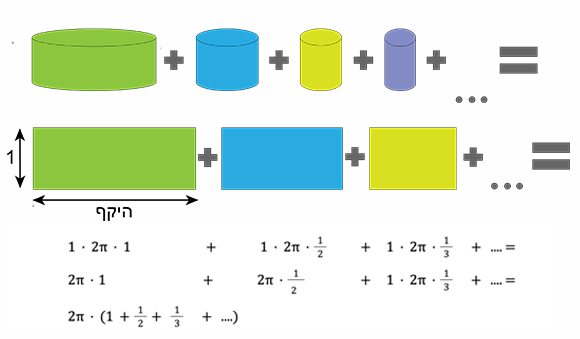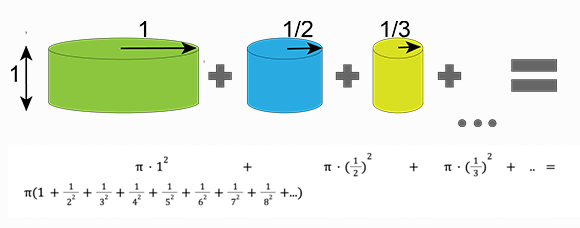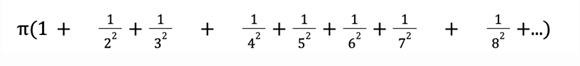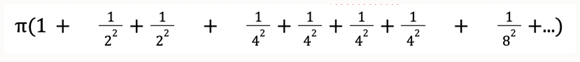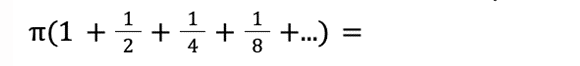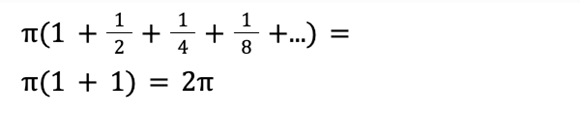יש סיבות טובות לכך שנדרשו לאנושות אלפי שנים להגיע אל האינסוף (המתמטי). אחת מהן היא שהוא מנוגד לאינטואיציה שלנו, ולכן המון תופעות שקשורות אליו נראות לנו פרדוקסליות, ולכאורה לא מתיישבות עם השכל הישר.
לאינטואיציה שמור מקום חשוב מאוד במתמטיקה. בניגוד למה שמספרים לפעמים, אי אפשר לעשות מתמטיקה רק כמשחק פורמלי של אקסיומות. או לפחות, אף אחד לא עושה ככה מתמטיקה. הרבה פעמים אנחנו צריכים קודם להרגיש מה אמור לקרות, אפילו אם אנחנו מתמטיקאים מקצועיים, ורק אחר כך אנחנו ניגשים לחקור את הנושא בכלים מתמטיים פורמליים. אך הבעיה היא שהאינטואיציה שלנו התפתחה בעולם הסופי, וכשאנחנו מנסים להשתמש בה כדי להבין עצמים אינסופיים מתקבלות תופעות מוזרות. אחת מהן היא עוגה – כזאת שאפשר לאכול, אבל אי אפשר לְצַפּוֹת בקרם מתוק וטעים.
18 צפייה בגלריה


עוגה שאפשר לאכול, אבל אי אפשר לְצַפּוֹת בקרם מתוק וטעים. עוגת יום הולדת בשכבות
(איור: יונת אשחר בעזרת Firefly )
רגע, מה? בואו נתרגם את זה לשפה מתמטית, לאו דווקא על מנת להסביר, אלא כדי לדבר במונחים ברורים ומפורשים יותר. אם כך, "עוגה שאפשר לאכול" היא "עוגה שהכמות שלה סופית", כלומר הנפח שלה סופי ולכן אפשר לאכול אותה. "עוגה שאי אפשר לצפות" היא עוגה שאם נרצה לכסות בקרם מתוק את כל המשטחים החיצוניים שלה – ה"למעלה" והצדדים שלה, נגלה שאין להם סוף. אם נרצה להשתמש במונחים עוד יותר מדויקים נדבר על שטח פנים אינסופי. אבל "שטח פנים אינסופי עם נפח סופי" איכשהו נשמע פחות מוצלח מ"עוגה שאפשר לאכול ואי אפשר לצפות". אז נישאר עם העוגות שלנו.
עוד כתבות באתר מכון דוידסון לחינוך מדעי:
האם יש יותר הריונות בגלל אוזמפיק ודומותיה?
תאי דם מצופים
צוללנית בבקבוק - שהיא גם רקדנית
העוגה
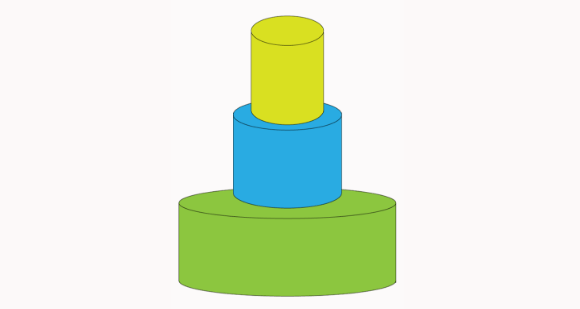
נדמיין עוגה. זה תמיד נחמד. עוגה עגולה, כמו בחתונות מהסרטים. כזאת עם קומות. הקומה הראשונה היא הכי פשוטה. זוהי פלטה עגולה בגובה של מטר אחד וברדיוס של מטר.
עכשיו נתחיל להוסיף קומות. כל הקומות יהיו באותו גובה, אבל כל אחת קצת יותר צרה מקודמתה. אז הקומה השנייה תהיה ברדיוס של חצי מטר:
הקומה השלישית תהיה שוב באותו גובה כמו קודמותיה, רק קצת יותר צרה. ברדיוס של שליש מטר:
וכך הלאה. רדיוס הקומה הבאה יהיה רבע מטר, זו שאחריה חמישית מטר וכן הלאה. אינסוף קומות! זה השלב שבו האינטואיציה שלנו עשויה לצעוק שזאת עוגה אינסופית, אז הכול בה אינסופי! יש אינסוף ממנה! ולכן גם כדי לצפות אותה צריך כמות אינסופית של קרם או קצפת. הכול אינסופי.
מתברר שזה לא נכון, וכדי להבין למה צריך קצת חישובים.
חישוב א': חימום
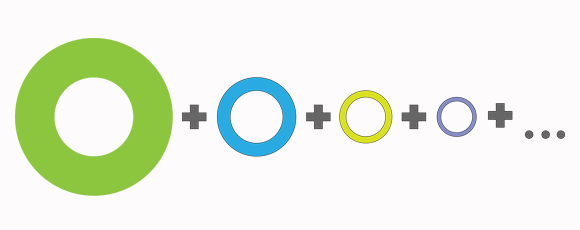
אז כתרגיל חימום בזמן שתנור האפייה מתחמם, נבדוק מה יקרה אם נרצה לצפות את העוגה רק מלמעלה. כלומר רק את טבעת הגג של כל שכבת עוגה. הנה, החלקים האלה:
לכאורה זה חישוב מסובך, כי יש לנו אינסוף טבעות לחבר.
למרבה המזל מספיק שינוי קל של נקודת המבט והשאלה הזאת נהיית הרבה יותר פשוטה. והפעם זה יהיה באמת שינוי של נקודת המבט, במובן הכי מילולי שאפשר: במקום להסתכל על העוגה מהצד נביט בה מלמעלה. ומלמעלה, העוגה האינסופית שלנו היא פשוט עיגול. עיגול אחד. כל הטבעות נכנסות בול זו בתוך זו, ויוצרות ביחד פשוט עיגול אחד שרדיוסו 1 מטר, כמו השכבה הראשונה.
ומהו שטחו של עיגול ברדיוס של מטר אחד? פאי, כמו שמתבקש כשמדברים על עוגות.
חישוב ב': ציפוי
אז ראינו שאת הגג של כל קומה אנחנו יכולים לצפות בלי קושי מיוחד. האם נוכל לצפות שנוכל לצפות את העוגה גם מהצדדים?
מבחינה הנדסית, כל דופן של שכבה היא המעטפת של גליל:
כשפורסים את המעטפת של גליל מקבלים מלבן. במקרה שלנו הגובה של כל מלבן כזה הוא כמו הגובה של כל אחת מהשכבות של העוגה – מטר אחד. האורך של כל מלבן כזה הוא היקף המעגל, ששווה למכפלה של פעמיים פאי ברדיוס המעגל. וכזכור, הרדיוסים שלנו הם 1, ½, ⅓ וכו'. לכן נקבל:
הסכום שבתוך הסוגריים, אחד ועוד חצי ועוד שליש וכו וכו, הוא סכום שידוע כ"טור הרמוני" – הדוגמה הקלאסית במתמטיקה לסכום שהאיברים שלו הולכים ומתכווצים, ועדיין הסכום הזה מצליח לגדול ולגדול ולגדול עד אינסוף. יש לזה הוכחה קטנה ולא מסובכת, אבל זה כבר באמת סיפור אחר.
כלומר גודל הציפוי הנחוץ לכיסוי דפנות העוגה שלנו, שהוא סכום המעטפות של הגלילים, שהוא סכום של מלבנים – הוא אינסופי. . וזה הגיוני: כשמסתכלים על העוגה מלמעלה רואים עיגול, ולכן הציפוי מלמעלה יוצא סופי. אבל כשמסתכלים על העוגה מהצד היא אכן נראית אינסופית, והגיוני שזה מה שיראה החישוב. אז אי אפשר לצפות את העוגה. כלומר, אפשר רק מלמעלה, אבל זה לא באמת נחשב ציפוי אם הוא לא מכסה יפה גם את דפנות העוגה, נכון?
חישוב ג': האם אפשר לאכול את העוגה?
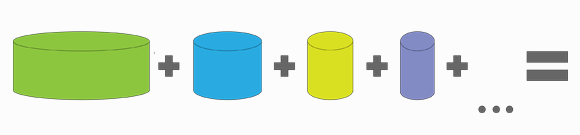
ועכשיו, לשאלה החשובה ביותר, שכדי לענות עליה צריך להבין כמה עוגה בעצם יש לנו. במונחים טיפונת יותר מדויקים נשאל מהו הנפח של העוגה.
השאלה הזאת לא נשמעת מסובכת. הרי העוגה אינסופית – כבר הראינו שבדיוק בגלל זה לא נוכל לצפות את כל דופנותיה. אז אם נמדוד לא רק את הדפנות אלא ממש את כל העוגה, כולל התוכן הטעים שלה, האם ייתכן שנגלה משהו שאינו אינסופי?
זה השלב שבו אנחנו נזכרים בהבטחה לעוגה שאי אפשר לצפות אבל אפשר לאכול. אז הבה נחשב. הגובה של כל גליל הוא מטר אחד, והרדיוסים הולכים וקטנים. נפח גליל הוא מכפלת הגובה בשטח הבסיס (פאי כפול הרדיוס בריבוע), ולכן נקבל:
עכשיו נעשה כמעשה הטווסים: נכביד על עצמנו. ניקח את הסכום הזה, שהוא כבר אינסופי באורכו, ונגדיל אותו עוד יותר. אבל נעשה את זה בצורה קצת מתוחכמת. ואז, אם נצליח להראות שהסכום המוגדל מתחבר ביחד לתוצאה סופית, הרי שקל וחומר שגם הסכום שלנו חייב להיות סופי.
כדי להגדיל אותו, ראשית נחלק את המחוברים לקבוצות:
כלומר האחד לבד, החצי בזוג, הרבע ברביעייה, השמינית יהיה בשמינייה וכן הלאה. עכשיו נגדיל את הסכום:
הקטנו את המכנים ולכן הגדלנו את הסכום: הרי חצי גדול יותר משליש, רבע גדול יותר מחמישית, שישית או שביעית, וכן הלאה. נחשב מה יצא.
לכן חילקנו דווקא לקבוצות האלה, והגדלנו את האיברים דווקא בצורה הזאת. כי עכשיו זה מצטמצם:
זה כבר סכום הרבה יותר פשוט, וגם הרבה יותר מוכר. ספציפית הסכום הזה:
אפשר לפתור אותו כסכום של סדרה הנדסית, אבל יש גם דרך חזותית הרבה יותר פשוטה להבין מה קורה פה. חצי ועוד רבע (חצי ממה שנשאר) ועוד שמינית (חצי ממה שנשאר) וחוזר חלילה, זה בעצם הדבר הבא:
וכך הלאה. בסופו של דבר כל הריבוע יתמלא. כלומר הסכום הזה, כשמושכים אותו עד לאינסוף כמו שאנחנו באמת אמורים לעשות, הוא בדיוק 1. אז 1 ועוד הסכום הזה זה פשוט 2. וקיבלנו:
עכשיו צריך להיזכר מה הסכום הזה מייצג ולמה רצינו לחשב אותו מלכתחילה. הסכום הזה הוא תוצאה של ההכבדה. כלומר הוא גדול יותר מסכום אחר – זה שמייצג את הנפח של העוגה. עשינו את זה כדי לדעת אם אפשר לאכול אותה. אם הנפח שלה קטן מ-2π, אנחנו אומנם לא יודעים מה הוא בדיוק, אבל ברור לנו שהוא לא אינסופי. באופן מאוד לא אינטואיטיבי, הנפח של העוגה הזאת, שיש לה אינסוף קומות, הוא סופי.
איך זה ייתכן?
מה קיבלנו?עוגה עם נפח סופי - כלומר שאפשר לאכול אותה, אבל שטח פנים אינסופי - שאי אפשר לצפות בציפוי. בקיצור, טעים אבל לא כל כך נעים.
את הסיפור הזה הגה בשנת 1681 המתמטיקאי אוונג'ליסטה טוריצ'לי (Torricelli), שבמקום עוגה דיבר על קרן יין. בעיקרון מדובר באותו דבר, פרט לכך שטוריצ'לי דיבר על קרן "חלקה", לא מחולקת לקומות: במקרה שלו יש לנו קרן שאפשר למלא במשקה ולשתות אותו עד תום, אך לא יעלה בידינו למרוח את המשקה על דופנותיה. המתמטיקה העקרונית היא אותה מתמטיקה, רק קצת יותר מסובכת כי אי אפשר לעשות סכומים נוחים מחולקים לקומות, וצריך להפעיל טכניקות סכימה מתוחכמות יותר. אבל לב העניין נשאר זהה.
למה זה קורה? בדיעבד זה אולי לא אמור להפתיע אותנו. נפח מתנהג, בגדול, כמו חזקה שלישית, ושטח כמו חזקה שנייה. והחזקה השלישית תמיד מהירה יותר: היא צומחת מהר יותר, אבל גם מתכווצת מהר יותר. זה אומר שכשהעוגה (או הקרן) מתכווצת, הנפח שלה מתכווץ במהירות רבה לאין שיעור משטח הפנים שלה. במקרה הזה הנדסנו את ממדי העוגה כך שהנפח שלה יתכווץ מהר מספיק כדי להיות סופי, אך לא שטח הפנים שלה. אפשר היה להנדס גם עוגות שבהן שני הדברים סופיים או אינסופיים, אבל אז איפה יהיה הכיף?
מיכאל גורודין, מכון דוידסון לחינוך מדעי, הזרוע החינוכית של מכון ויצמן למדע