מהנדסים מהמכון הטכנולוגי של קליפורניה (Caltech) גילו שהבנתו של לאונרדו דה וינצ'י את כוח המשיכה - אם כי לא לגמרי מדויקת - הקדימה את זמנו בכמאה שנים ויותר. "לפני כ-500 שנים, לאונרדו דה וינצ'י ניסה להבין את תעלומת הכבידה ואת הקשר שלה להאצה באמצעות סדרה של ניסויים גאוניים, שבוצעו בפועל רק על ידי דמיונו וטכניקות ניסוי מופתיות שלו", אמרו החוקרים על איש האשכולות שידע כי מצא משהו, אבל הוא לא היה בטוח בדיוק במה מדובר.
במחקר, שפורסם בכתב העת Leonardo, הסתמכו החוקרים על אחת המחברות של דה וינצ'י על מנת להראות שאיש האשכולות המפורסם הגה ניסויים כדי להוכיח שכוח המשיכה הוא סוג של תאוצה, תוך שהוא מעצב עוד יותר את קבוע הכבידה - קבוע פיזיקלי אמפירי שמסומן באות G ומבטא את הקשר בין גודלה של מסה לבין עוצמת תופעות הכבידה שהיא מחוללת במרחב בהתאם למרחק ממנה - לדיוק של כ-97%.
דה וינצ'י, שחי מ-1452 עד 1519, הקדים בהרבה את התקופה שבה התפתח חקר המושגים הללו, זאת לאור העובדה כי רק בשנת 1604, גלילאו גליליי העלה תיאוריה לפיה המרחק שעובר עצם נופל הוא פרופורציונלי לריבוע הזמן שחלף (כלומר שגוף הנופל מכל נקודה שהיא על מעגל מאונך, יגיע לנקודה הנמוכה ביותר במעגל בזמנים שווים), ורק בסוף המאה ה-17 סר אייזק ניוטון הרחיב על חוק הכבידה האוניברסלי שקובע כי כל שני גופים בעלי מסה נמשכים זה לזה ביחס ישר למכפלת מסותיהם, וביחס הפוך לריבוע המרחק ביניהם. למעשה, המכשול העיקרי שניצב בדרכו של דה וינצ'י היה שהכלים שעמדו לרשותו היו מוגבלים, שכן חסר לו אמצעי למדידת הזמן המדויק שחולף מרגע נפילת עצם כלשהו מטה.
הניסויים של דה וינצ'י זוהו לראשונה על ידי מורטזה עריב, פרופ' להנדסת אווירונאוטיקה והנדסה רפואית, שחקר את הקודקס ארונדל (Codex Arundel), אוסף מאמרים בן 283 עמודים - הקרוי על שמו של הרוזן מארונדל, שרכש אותו בספרד בשנות ה-30 של המאה ה-17. מדובר במאמרים שנכתבו על ידי דה וינצ'י, בעיקר בין השנים 1480 עד 1518, ומכסים מגוון תחומים כולל מדע, אמנות ונושאים אישיים.
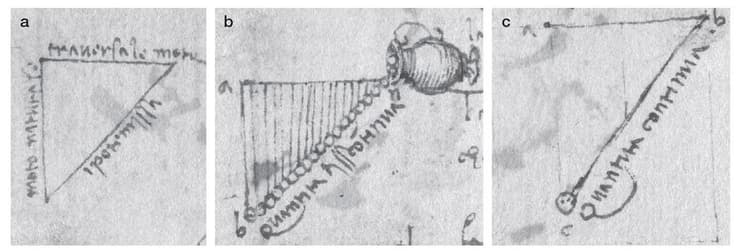
בתחילת 2017, פרופ' עריב חקר את הטכניקות של דה וינצ'י להדמיית זרימה, לאחר שהבחין בקודקס ארונדל, שאת חלקו העלתה לרשת הספרייה הבריטית, בסדרה של סקיצות המציגות משולשים שנוצרו על ידי חלקיקים דמויי חול שנשפכים מתוך כלי קיבול. "מה שמשך את עיניי היה הכיתוב 'משוואות תנועה' (Equatione di Moti) על החלק התחתון של אחד המשולשים המשורטטים של דה וינצ'י - זה שהיה משולש ישר זווית שווה שוקיים", אמר עריב, המחבר הראשי של המחקר, אשר הסתקרן להבין למה דה וינצ'י התכוון בביטוי זה.
כדי לנתח את ההערות הכתובות של דה וינצ'י, עבד פרופ' עריב עם עמיתיו כריס רו, בזמנו חוקר פוסט-דוקטורט במכון הטכנולוגי של קליפורניה וכיום עוזר פרופ' באוניברסיטת קורנל, כמו גם עם פלאביו נוקה מהאוניברסיטה למדעים שימושיים ואמנויות בשוויץ. נוקה סייע בתרגום הערותיו האיטלקיות של דה וינצ'י, כששלושת החוקרים התעמקו יחדיו בדיאגרמות של כתב היד. דה וינצ'י תיאר בכתביו ניסוי שבו כד הוזז לאורך נתיב ישר ומקביל לקרקע, תוך מזיגת חומר גרגירי (ככל הנראה חול) לאורך המסלול.
מהערותיו עלה כי היה מודע לכך שתכולת הכד לא תישפך במהירות קבועה, אלא באופן מואץ מטה, מכורח כוח הכבידה, שכן אם הכד נע במהירות קבועה, הקו שנוצר על ידי נפילת החומר שהכיל היה אנכי, כך שלא נוצר משולש, אך אם הוא נע במהירות מואצת, הקו שנוצר על ידי החומר הנשפך ממנו יצר קו ישר אך אלכסוני, שהרכיב בסופו של דבר משולש. דה וינצ'י ציין באחד מתרשימי המפתח בקודקס, כי אם תנועת כלי הקיבול מואצת באותו קצב שבו כוח הכבידה מאיץ את החומר הנשפך מטה, הדבר יוצר משולש שווה צלעות - ממש כפי שפרופ' עריב שם לב שאיש האשכולות האיטלקי, שהיה מגדולי אמני הרנסאנס, הדגיש כשכתב "Equatione di Moti", כלומר "משוואות תנועה" - תיאור מתמטי להתנהגות של מערכות פיזיקליות המציגות את התנועה כתלות בזמן - במה שדמה לעיקרון השקילות של אלברט איינשטיין משנת 1907 לפיו ישנו שוויון פיזיקלי לוקאלי בין תאוצה וכבידה.
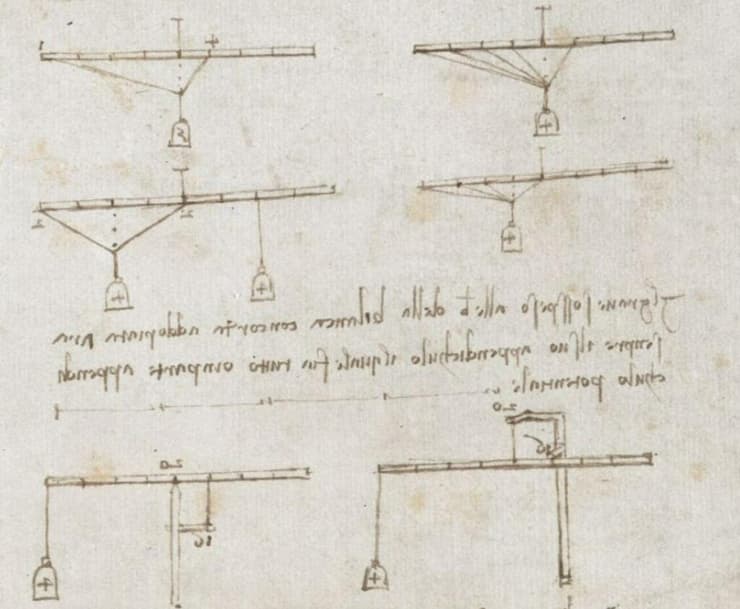
למעשה, דה וינצ'י רצה לתאר באופן מתמטי את התאוצה הזו, אם כי במקרה הזה, כך על פי מחברי המחקר, הוא לא בא על מבוקשו. כדי לחקור את התהליך שעשה דה וינצ'י, השתמשו חברי הצוות במודלים ממוחשבים כדי להמחיש את הניסוי שלו על ידי שימוש באגרטל מים והבינו כי עקרון האינרציה - שבו חפצים ממשיכים לנוע בכיוון אחד עד שהם נתקלים בכוח מנוגד - עדיין לא התבסס במדע של אותה תקופה, מה שגרם לחוסר וודאות אצל דה וינצ'י. "אנחנו לא יודעים אם דה וינצ'י עשה ניסויים נוספים או בדק את הנושא לעומק, אבל העובדה שהוא עשה זאת בתחילת המאה ה-15 רק מוכיחה עד כמה החשיבה שלו הייתה מפותחת ומתקדמת לאותה העת", סיכם פרופ' עריב.