ג'ינאון בק, מתמטיקאי מאוניברסיטת יונסיי בקוריאה, טוען כי פתר את "בעיית הזזת הספה". הוא פרסם הוכחה באורך של מעל 100 עמודים בשרת ה-preprint של arXiv.
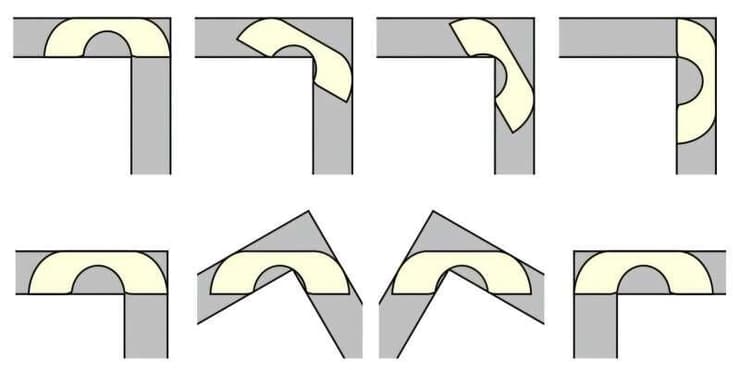
"בעיית הזזת הספה" הוצעה לראשונה על ידי המתמטיקאי הקנדי ליאו מוזר בשנת 1966. מוזר ניסח את השאלה כחידה גיאומטרית פשוטה לכאורה: מהו השטח המקסימלי של צורה מישורית שיכולה להסתובב ולעבור דרך מסדרון בצורת "L" ברוחב יחידה אחת? הבעיה, שזכתה לכינוי "בעיית הזזת הספה", הפכה מאז לאתגר מתמטי קלאסי, המשלב גיאומטריה, אופטימיזציה, וניתוח חישובי מתקדם.
במהלך השנים הוצעו צורות שונות כפתרונות אפשריים. הצורה המובילה עד היום, המכונה "הספה של גרבר", פותחה בשנות ה-90 של המאה הקודמת ומורכבת מ-18 עקומות מתמטיות. עם זאת, אין הוכחה מוחלטת לכך שזו הצורה המקסימלית האפשרית. הבעיה ממשיכה לעורר עניין בקרב חוקרים, ומשמשת דוגמה לחשיבות של חשיבה יצירתית וכלים חישוביים מתקדמים במתמטיקה המודרנית.
רוב האנשים שעברו דירה נתקלו ב"בעיית הזזת הספה" – היא מתעוררת כאשר מנסים להעביר ספה דרך פינה במסדרון. השאלה היא: מהי הספה הגדולה ביותר שניתן להעביר דרך פינה נתונה מבלי להיתקע? בעיה זו הוצגה לראשונה באופן מתמטי על ידי המתמטיקאי ליאו מוזר בשנת 1966, ומאז ועד היום נותרה בלתי פתורה.
באתר phys.org נכתב כי מחשבותיו הראשוניות של מוזר התרכזו באפשרות לפתח הוכחה שתראה כיצד ניתן להשתמש במתמטיקה כדי לפתור בעיה כזו באמצעות צורה מישורית נתונה, כאשר היא מועברת סביב פינה בזווית ישרה בתוך חלל ריק (כמו מסדרון) ברוחב יחידה אחת.
בעבודתו, בחר בק להשתמש ב"ספת גרבר" כצורה להדגמה. ספת גרבר היא מבנה מתמטי שפותח על ידי ג'וזף גרבר, פרופסור מאוניברסיטת רטגרס, בשנת 1992. למעשה, מדובר בצורת קובואיד (מלבן תלת-ממדי) עם חזית בצורת U, גב שטוח עם פינות מעוגלות וזרועות שטוחות הפונות קדימה.
לאחר שהגדיר את הבעיה באופן ברור, השתמש החוקר הקוריאני בכלים מתמטיים כדי להתקדם שלב אחר שלב בהוכחה, עד שהגיע לתשובה: עבור מסדרון ברוחב יחידה אחת, השטח המקסימלי של ספת גרבר יכול להיות 2.2195 יחידות בלבד. כחלק מההוכחה, בק גם הגדיר באופן מדויק את צורת ספת גרבר שבה השתמש. לכן, פרשנויות שונות לצורת הספה עשויות להוביל לתשובות שונות.
כמו בכל הוכחה מתמטית כזו, הוכחתו של בק תצטרך לעבור בדיקה מעמיקה על ידי מתמטיקאים אחרים כדי להבטיח שההוכחה נכונה ושהיא אכן מובילה לפתרון האופטימלי לבעיה נתונה.
