יצאתם לטיול והגעתם למקום חדש שלא הייתם בו מעולם בו - נוף חדש. כדי לתאר את המאפיינים העיקריים של תוואי הנוף תחפשו ודאי נקודות ציון בולטות בשטח, למשל ההר הגבוה ביותר, הנקודה העמוקה ביותר בעמק, וכן הלאה.
הדבר דומה גם להתמצאות בחלל, פרט לכך ששם תוואי הנוף הוא מיוחד: לא של תוואי שטח, אלא של תוואי אנרגיה במערכת מסתובבת של שני גופים שחגים במסלול זה סביב זה. נשמע מסובך, אבל זה בעצם פשוט, ונסביר את זה מיד. העיקר הוא שנקודות השיא האלה, הקרויות נקודות לגראנז', הן נקודות שקל מאוד להישאר בהן זמן רב בלי להתאמץ. לכן, כשמסתכלים על מערכת השמש שלנו מגלים בנקודות האלה אלפי אסטרואידים, וגם כמה חלליות מעשה ידי אדם, חלקן מפורסמות למדי – כמו טלסקופ החלל ג'יימס ווב.
מה אפשר ללמוד מכדור וקערה?
אם נניח כדור במקום כלשהו בתוך קערה, הוא יתגלגל מטה וייעצר בסופו של דבר בתחתיתה. זה קורה כי הכדור שואף להגיע לנקודה שבה יש לו הכי מעט אנרגיה – כלומר למטה. לכן, כל עוד הוא נמצא על משטח משופע, הוא ינצל את האפשרות להתגלגל לנקודה נמוכה יותר. בסופו של דבר הוא ייעצר רק כשיגיע למשטח אופקי, כלומר לתחתית הקערה, או בשפה קצת יותר מתמטית: לנקודת המינימום של האנרגיה. זהו שיווי משקל יציב – הכדור יישאר בו לאורך זמן, וגם אם נזיז אותו הצידה הוא יתגלגל מחדש לאותה נקודת מינימום.
עוד כתבות באתר מכון דוידסון לחינוך מדעי:
קופצים למסקנות: על צפרדעים, אגדות אורבניות והסקה מדעית
מחלות ללא גבולות - קדחת דנגי עוברת את הגבול
הגֵנים שמוציאים את הזכרים מהעסק
עכשיו נהפוך את הקערה על ראשה. גם כאן יש מקום שבו המשטח אינו משופע – זו בעצם אותה נקודה בדיוק, רק שעכשיו היא נקודת מקסימום של האנרגיה, לא נקודת מינימום. המשמעות היא שאם נניח את הכדור בזהירות רבה מאוד בדיוק בנקודת המקסימום, הוא אכן יישאר שם. אבל הפעם שיווי המשקל שלנו איננו יציב: כל תזוזה קטנה תביא את הכדור למשטח משופע, ואנחנו כבר יודעים שבמשטח כזה הוא יתגלגל תמיד למטה, הרחק מנקודת המקסימום.
את הרעיון הזה אפשר להכליל: בכל מקום שיש בו נקודת קיצון של אנרגיה – כלומר מינימום או מקסימום – תהיה נקודת שיווי משקל. יכולות להיות נקודות רבות כאלה – חישבו למשל כמה נקודות מינימום ומקסימום יש בקרטון ביצים.
6 צפייה בגלריה


הכדור תמיד ייעצר בסוף בתחתית הקערה, נקודת המינימום של האנרגיה שלו
( איור באמצעות DALL-E )
נקודות לגראנז' הן נקודות קיצון של אנרגיה, ומכאן שהן נקודות שיווי משקל. במקרה הזה שיווי המשקל הוא זה הנוצר במערכת של שני גופים שמושכים זה את זה וחגים זה סביב זה. ומכיוון שאלה נקודות שיווי משקל, אם נניח בהן גוף שלישי הוא פשוט יישאר באותו מקום ולא יזוז, אף על פי ששני הגופים מושכים אותו אליהם כל הזמן.
שיווי משקל במקומות בלתי צפויים
היכן נמצאות בפועל הנקודות הללו? הבה נדמיין לרגע את כדור הארץ והירח ניצבים זה מול זה. אם נניח גוף כלשהו קרוב לכדור הארץ, הוא ייפול אליו, ואם נניח אותו קרוב לירח הוא ייפול לירח. אבל אי שם בין כדור הארץ לירח יש נקודה אחת שבה כוח המשיכה של כדור הארץ שווה בדיוק לכוח המשיכה של הירח. אם נניח את הגוף הקטן שלנו בנקודה הזאת, הוא פשוט יישאר בה ולא יזוז – כלומר יהיה בשיווי משקל. זהו קו המחשבה שמאפשר לזהות את נקודות לגראנז'.
לתיאור הפשוט הזה צריך להוסיף את העובדה שהירח וכדור הארץ לא עומדים במקום, אלא נעים כל הזמן וחגים יחד סביב מרכז הכובד המשותף שלהם. אם נעבור כעת להסתכל במערכת המסתובבת כאילו גם אנחנו חגים בתוכה, שני הגופים יחזרו להיראות נייחים ביחס אלינו, אבל אסור לשכוח שאנו מסתובבים עכשיו בעצמנו, כלומר נמצאים בתאוצה.
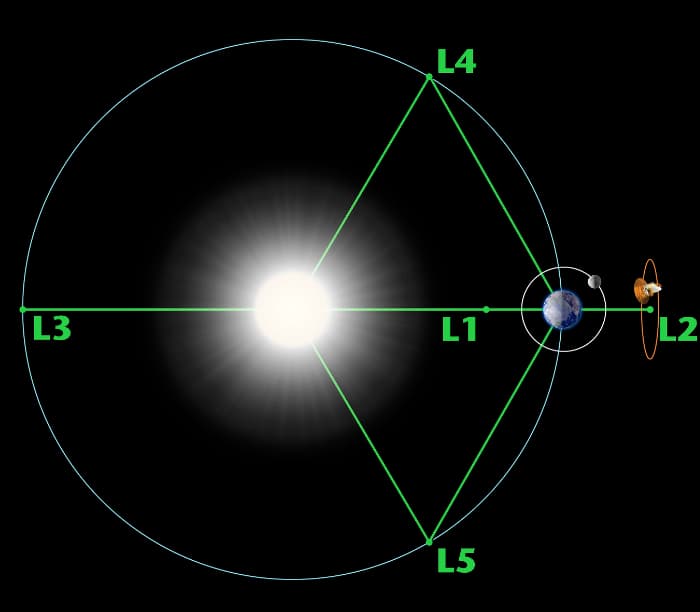
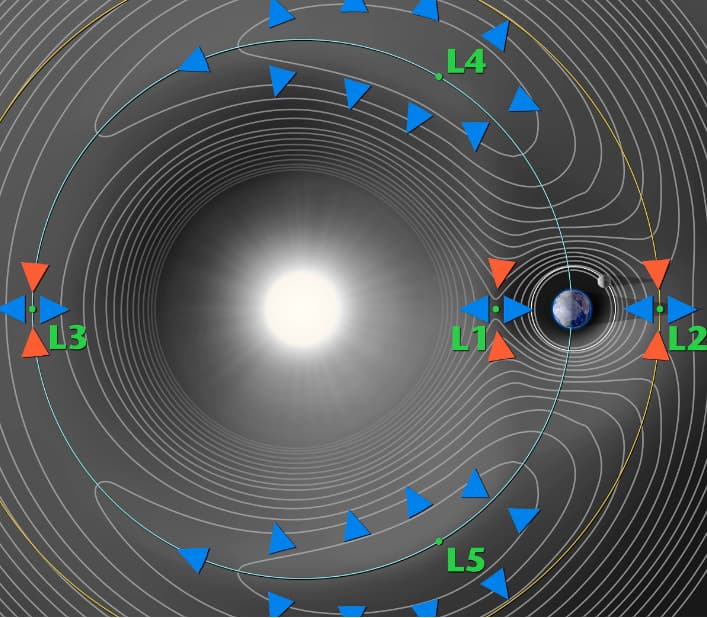
הדרך לעשות את זה היא להוסיף לחישובים את הכוח הצנטריפוגלי, שהוא כוח "דמיוני" במובן זה שאף אחד לא מפעיל אותו, אבל הוספתו מאפשרת לבטא את זה שבחרנו להסתכל על העולם ממערכת מסתובבת. כשהמתמטיקאי הצרפתי ז'וזף-לואי לגראנז' (Lagrange) חישב את זה ב-1772 הוא גילה שבמערכת כזאת יש לא רק נקודת קיצון אחת, אלא חמש נקודות שיווי משקל קבועות במערכת המסתובבת, כלומר מסתובבות יחד עם הגופים. שלוש הראשונות נמצאות על הקו הישר המחבר בין הגופים או על המשכו. L1 היא הנקודה שבין הגופים, בדומה לזאת שדמיינו קודם בין כדור הארץ והירח; L2 נמצאת מחוץ למסלול בדיוק מעבר לגוף המשני; ו-L3 נמצאת בדיוק מאחור, מעבר לגוף הראשי. שתי הנקודות האחרות, L4 ו-L5, נמצאות על המסלול של הגוף המשני, אך בזווית של 60 מעלות לפניו או אחריו בהתאמה.
6 צפייה בגלריה
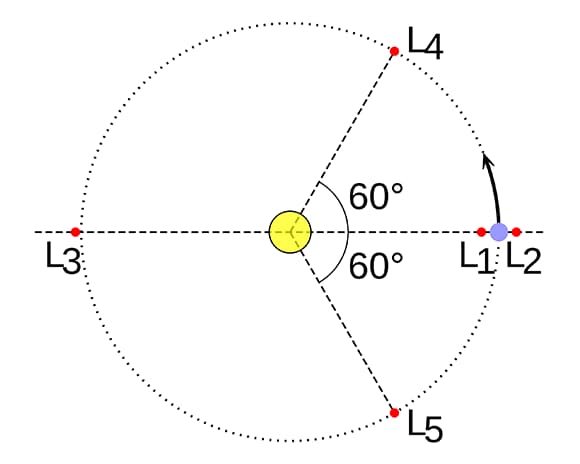

מקומן של חמש נקודות שיווי המשקל שקיימות בכל מערכת של שני גופים שחגים זה סביב זה עקב כוח המשיכה ביניהם. בצהוב: הגוף הראשי; בסגול: הגוף המשני
(איור: EnEdC, ויקיפדיה, נחלת הכלל)
בחיפוש אחרי הנקודות הללו תיאר לגראנז' את האנרגיה שתהיה לחלקיק בכל נקודה ונקודה, ואז חיפש את נקודות קיצון של תוואי האנרגיה. זהו כמובן תיאור פשוט יותר ממה שקורה בפועל: במציאות המסלולים אינם מעגלים מושלמים אלא אליפסות, ויש כוחות משיכה נוספים שפועלים במערכת מעבר לזוג שמעניין אותנו – למשל השמש, צדק וכן הלאה, ולכל זוג יש נקודות לגראנז' משלו. התוצאה היא שאין באמת נקודות שיווי משקל מושלמות – אבל האזורים הסמוכים לנקודות לגראנז' אכן יציבים במיוחד.
בזכות היציבות הזאת, גופים שמגיעים לסביבתן של נקודות לגראנז' נוטים להישאר בה, כך שנקודות לגראנז' גם מופיעות באופן מוחשי בטבע. דוגמה טובה במיוחד היא ריבוי האסטרואידים שנמצאים באזור נקודות L4 ו-L5 של מערכת שמש-צדק: יותר מ-10,000 אסטרואידים ידועים, שמכונים "אסטרואידים טרויאנים", שוכנים שם – ממש על מסלולו של צדק סביב השמש, אבל קצת לפני כוכב הלכת או אחריו. אפילו לכדור הארץ הקטן שלנו יש שני אסטרואידים טרויאנים מוכרים משלו.
6 צפייה בגלריה


אסטרואידים במערכת השמש הפנימית. בלבן: חגורת האסטרואידים; בירוק: האסטרואידים הטרויאניים של מערכת שמש-צדק, מחולקים לשני מחנות: המכונים "יוונים" ו"טרויאנים", אם כי כולם מוגדרים אסטרואידים טרויאניים
(תרשים: Mdf, ויקיפדיה, נחלת הכלל)
מקום סביב השמש
הנקודות L1 ו-L2 של המערכת שמש-כדור הארץ נמצאות כ-1.5 מיליון ק"מ פנימה או החוצה ממסלולו של כדור הארץ, ושתיהן שימושיות עבורנו. חללית שמשוגרת ל-L1 חשופה תמיד לאור השמש מצידה האחד, ולצד המואר של כדור הארץ – צד היום – מעברה האחר. כיום יש שם ארבע חלליות פעילות, וארבע נוספות נשלחו לשם בעבר.
נקודת לגראנז' L2 מיוחדת בכך שכל מקורות האור הגדולים בסביבתה – השמש, הירח וכדור הארץ עצמו – נמצאים פנימה לעומתה. לכן זה מקום מצוין להציב בו טלסקופי חלל שיימנעו מהסנוור שלהם וישקיפו אל כוכבי השמיים החיוורים בכיוון הרחוק מהשמש. ארבע החלליות שנמצאות שם – וביניהן טלסקופ החלל ג'יימס וב – בדומה לחמש החלליות הנוספות ששוגרו לשם בעבר, נהנות מתנאי סביבה יציבים במיוחד, וכן מתקשורת קלה עם כדור הארץ שתמיד נמצא מבחינתן בערך באותו מקום.
בפועל, החלליות הללו לא נמצאות ב-L2 ממש אלא רק מקיפות את הנקודה במרחק מה ממנה, מאחר שהנקודה עצמה נמצאת תמיד בצילו של כדור הארץ, בדומה לירח במהלך ליקוי. החלליות הללו צריכות אור שמש להפקת חשמל, אז הן נעות במסלול יציב למדי בחלל לא הרחק מנקודת לגראנז' השנייה, ומקיפות אותה, אבל לא נמצאות בדיוק בה.
נקודת לגראנז' השלישית במערכת הזו, L3, היא נקודה שאנו עיוורים לה לגמרי מכדור הארץ, מאחר שהשמש תמיד נמצאת בינינו לבינה. במשך השנים העובדה הזאת שימשה כר פורה להשערות פרועות על גופים חלליים גדולים שמסתתרים שם – אפילו כוכב לכת שלם – ותורות קונספירציה על דברים שגורמים עלומים הסתירו שם מעינינו. אך אל דאגה, חלליות שהתרחקו מכדור הארץ צילמו את האזור כולו ישירות – ולא מוסתר שם כלום.
בעתיד הרחוק יותר יש אפילו יוזמות להקים מושבות ענק, שיוכלו להלכה לאכלס מיליוני אנשים, בנקודות לגראנז' L4 ו-L5 של המערכת כדור הארץ-ירח. למעשה, מייסד חברת אמאזון ג'ף בזוס הקים כבר לפני יותר מעשרים שנה את חברת Blue Origin שזו מטרת העל ארוכת הטווח שלה. כך שאין ספק שהניתוח המתמטי של אחד המדענים הגדולים של המאה ה-18 תורם לחיים ולמדע של בני האדם במאה ה-21, ויתרום עוד בעתיד.
ד"ר אביב אופיר, מכון דוידסון לחינוך מדעי, הזרוע החינוכית של מכון ויצמן למדע