דוב אחד הלך דרומה קילומטר בקו ישר, פנה מערבה ושוב הלך קילומטר בקו ישר, פנה צפונה ושוב הלך קילומטר בקו ישר, והגיע חזרה לנקודה שממנה יצא. מה צבע הדוב?
זאת חידה מוכרת למדי. יש לה תשובה נכונה מקובלת אחת, אינסוף תשובות נוספות עם קצת התחכמות, ואפס תשובות נכונות כשבוחנים את הסוגיה קצת יותר בזהירות.
7 צפייה בגלריה


צועד כה וכה במעגלים ומגיע לאן? דוב לבן
(איור: shutterstock, עיבוד תמונה: מכון דוידסון)
התשובה הנכונה
נתחיל מהתשובה השכיחה (אך לא מדויקת), שהולכת בערך ככה: כשאנחנו מדמיינים את מסלולו של הדוב נוצר תרשים כזה, רק שאיכשהו נקודת ההתחלה ונקודת הסיום צריכות להתחבר. לכאורה זה בלתי אפשרי, עד שנזכרים שאנחנו לא חיים על מפה שטוחה, אלא על כדור. לכן הדוב התחיל בקוטב הצפוני. הוא הלך דרומה קילומטר, פנה שמאלה והלך מערבה קילומטר, ואז הלך צפונה קילומטר. כיוון שלכל אורך ההליכה שלו מערבה הוא נשאר במרחק קילומטר מהקוטב, כשהוא הלך צפונה הוא חזר לקוטב הצפוני, כלומר לנקודת ההתחלה שלו. אה, והדוב הוא לבן, כמובן, כי הוא גר בקוטב.
עוד כתבות באתר מכון דוידסון לחינוך מדעי:
מולקולת העתיד
התאים שמזקינים את הגוף
הרעל המסרטן של חיידק המעיים
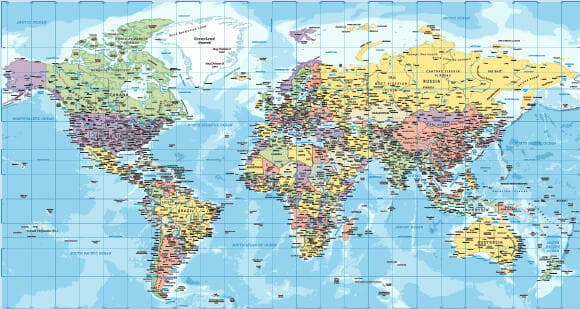
אנחנו מכירים את התופעה הזאת מהמפות שבהן כל הקוטב הצפוני "מרוח" על החלק העליון של המפה, ושתי נקודות שנראות רחוקות על המפה הן כמעט צמודות זו לזו במציאות.
איפה נמצא הקוטב הצפוני במפה כזאת? הוא צריך להיות איכשהו בכל המשבצות העליונות בעת ובעונה אחת. זה מה שקורה כשמציירים מפה של כדור על משהו דו-ממדי כמו מלבן: מוכרח להיות עיוות כלשהו, ואחת האפשרויות הקלות והנפוצות ביותר היא "למתוח" את המפה ככל שמתרחקים מקו המשווה.
אינסוף תשובות נכונות!
המתחכמים יוכלו למצוא לא רק תשובה אחת, אלא אינסוף: הטריק הוא ליצור מצב שבו ההליכה מערבה לא מזיזה אותנו מהמקום. כשהולכים מערבה על פני כדור הארץ אנחנו הולכים חלק ממסלול מעגלי. אם המסלול הזה קרוב מספיק לאחד הקטבים, הליכה של "קילומטר מערבה" תשלים מעגל שלם. לכן, אם נתחיל בנקודה שהיא צפונית בקילומטר מהמסלול המעגלי הזה – ומשם נלך דרומה, נפנה מערבה ונלך עוד קילומטר – בסוף ההליכה מערבה נחזור לנקודה שבה התחלנו ללכת מערבה, וכדי לחזור לנקודת ההתחלה של המסע כולו עלינו ללכת קילומטר צפונה. כעת כבר אי אפשר לדעת מה הצבע של הדוב, כי מסלול כזה אפשר לערוך רק ליד הקוטב הדרומי, ורגע, האם בכלל יש שם דובים?
אז איך זה שיש אינסוף פתרונות? ראשית, כי עלינו למקם את נקודת ההתחלה במרחק של קילומטר מצפון למסלול המעגלי הסגור שלנו, ויש אינסוף נקודות כאלה. שנית, המעגל שאנחנו צועדים בו הוא מעגל בהיקף של קילומטר. לכן כשאנחנו הולכים קילומטר מערבה אנחנו משלימים את כל המעגל. אבל קצת מתחתיו, קרוב יותר לקוטב הדרומי, יש מעגל שההיקף שלו הוא חצי קילומטר. כשנלך קילומטר מערבה לאורך המעגל הזה נשלים שתי הקפות שלו, ושוב ההליכה מערבה תחזיר אותנו למקום שבו התחלנו. אם נמקם את נקודת ההתחלה שלנו קילומטר אחד צפונית למעגל הקטן יותר, גם המסלול הזה יחזיר אותנו בדיוק לנקודת ההתחלה, פשוט נשלים שני סיבובים מערבה במקום אחד.
מובן שקצת דרומה משם יש מעגל קטן עוד יותר שהיקפו שליש קילומטר, ואם נתמקם קילומטר אחד מצפון לו ונלך מערבה, נשלים שלושה סיבובים ושוב נחזור בדיוק למקום שבו התחלנו. אפשר להמשיך את הניסוי המחשבתי הזה עם מעגל שהיקפו רבע קילומטר, חמישית קילומטר וכן הלאה; מבחינה מתמטית טהורה קיימים אינסוף מסלולים כאלה.
7 צפייה בגלריה

אינסוף פתרונות נכונים למתחכמים, הליכה מערבה משלימה סיבוב סמוך לקוטב הדרומי
(איור: shutterstock, עיבוד תמונה: מכון דוידסון)
אבל למעשה, אף תשובה אינה נכונה
הבעיה היא שאף אחד מהפתרונות האלה לא באמת נכון, והסיבה לכך היא מילה אחת שנדמה לנו שאנחנו מבינים היטב, אבל זה לא המצב. נסו לקרוא שוב את השאלה המקורית ולחשוב מה יכול להיות אותו מושג חמקמק, אותה מילה מתעתעת.
מוכנים? קראתם? יכול להיות שחלק מכם זיהו את המילה "ישר". אינטואיטיבית נראה שאי אפשר בכלל לדבר על קווים ישרים, כי כשאנחנו על כדור עגול ולא על מפה שטוחה, מה זה בכלל "ללכת ישר דרומה"? דרומה זה לא ישר! זה מסלול קמור במקצת, כי הוא על פני כדור הארץ. אבל למעשה זאת לא בעיה בכלל. כלומר, זה מתחיל להיות קצת בעייתי כשפונים מערבה.
כדי לדבר על קווים ישרים על משטח כדורי דרושה הגדרה מדויקת. מה זה בעצם "קו ישר"? במישור אפשר להתייחס לקו ישר בשתי דרכים שונות. אף על פי שלעיתים נחשוב על "ללכת ישר" בתור "ללכת בלי פניות", מסתבר שיש הגדרה אחרת, חשובה יותר: "ללכת ישר" משמעו ללכת בדרך הקצרה ביותר שמחברת בין שתי נקודות. לדרך כזו קוראים מסילה גיאודזית. שתי ההגדרות האינטואיטיביות האלה מתלכדות במישור שטוח, אבל הן יכולות להתיישב זו עם זו גם במשטחים עקומים, אם הם מספיק "נחמדים".
כדור הוא משטח נחמד כזה. כשאנחנו על כדור, מסילות גיאודזיות תמיד נמצאות על "מעגלים גדולים", כלומר על המעגל הגדול ביותר שמקיף את הכדור (כמו קו המשווה). הדרך הקצרה ביותר בין שתי נקודות על כדור תמיד תהיה מונחת על המעגל הגדול שעובר דרכן. כדי למצוא את המסלול הקצר ביותר בין שתי נקודות שנמצאות על אותו מעגל גדול, אפשר פשוט ללכת לאורך היקף המעגל שביניהן. אבל אפשר למצוא אותו גם על בסיס העיקרון "ללכת בלי פניות". אם ניסע לאורך מעגל גדול מסוים, ונמשיך בנסיעה בלי להזיז את ההגה – הנסיעה תהיה על היקף המעגל.
כל קווי האורך של כדור הארץ נמצאים על מעגלים גדולים, כי הם עוברים דרך שני הקטבים. אבל קווי הרוחב אינם כאלה. הם לא עוברים דרך הקטבים, ולמעשה, על פי ההרחבה למושג "קו ישר" שעשינו עבור כדורים, הם לא "ישרים". אומנם ראינו שאפשר להגדיר קו ישר בצורה שתתאים גם למשטחים מעוקמים, אבל חשוב לדעת לאיזה כיוון הם מתעקמים. קווי האורך מתעקמים רק "פנימה", כלומר, ביחד עם העקמומיות של הכדור שעליו הם ממוקמים, וזו הסיבה שכשנוסעים לאורך קו כזה אין צורך להזיז את ההגה – המסלול מתאים את עצמו למשטח. קווי הרוחב, לעומת זאת, מתעקמים גם "הצידה", כלומר, העקמומיות הנוספת שלהם לא תואמת את העקמומיות של הכדור. למעשה, כדי ללכת על קו רוחב צריך כל הזמן לזוז הצידה.
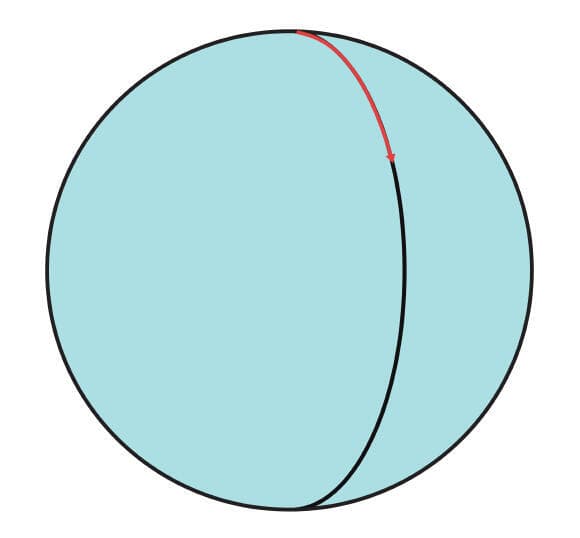
איך מסבירים את התופעה הזו בלי חישובים מסובכים? לשם כך כדאי להבין באיזה מובן מתוארים "מעגלים גדולים" כ"ישרים" על הכדור. אם נתחיל ללכת בכיוון כלשהו ונמשיך ישר בלי לסטות לצדדים, נקיף את הכדור לאורך מעגל גדול כזה. למשל כך:
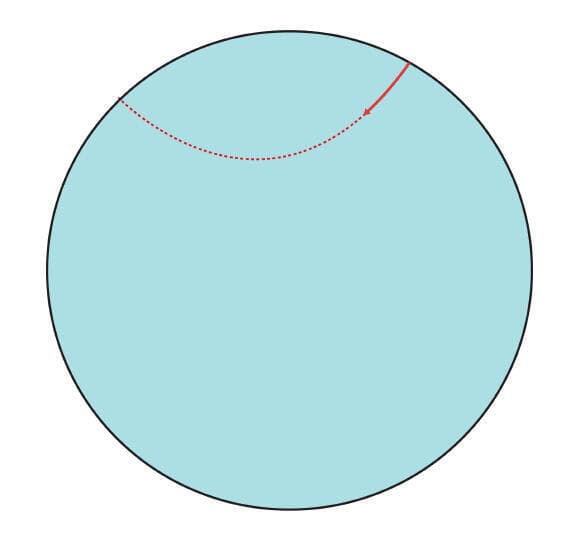
אז למה קו רוחב לא עובד ככה? הרי גם הוא מעגל על כדור:
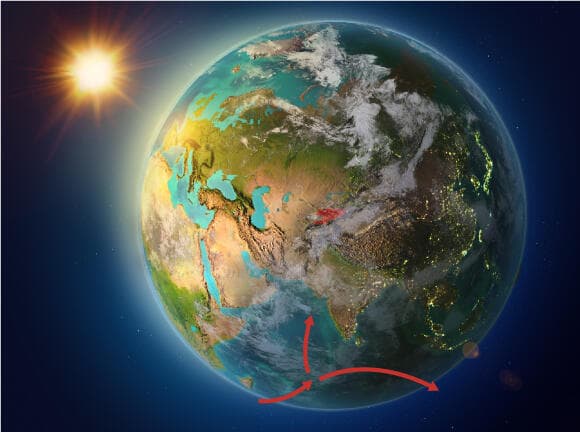
לפעמים שינוי נקודת המבט עוזר לנו להבהיר סוגיות מתמטיות. הבה נשנה את נקודת המבט – נסובב את הכדור כך שנקודת ההתחלה תהיה בקוטב הצפוני, ונוסיף את ה"קווים הישרים" שיוצאים ממנה:
7 צפייה בגלריה
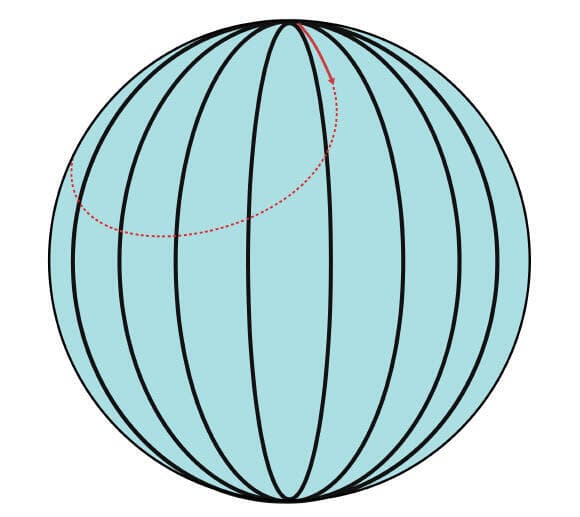

קווי אורך וקו מעגלי המתחיל בקוטב הצפוני
(איור: shutterstock, עיבוד תמונה: מכון דוידסון)
התחלנו ללכת "ישר דרומה" כמו קודם, אבל במקום להמשיך "ישר" דרומה, המסלול התעקל ימינה. כלומר, אפשר לראות בבירור שמעגל קטן על כדור יכול להתחיל באותה נקודה כמו "קו ישר", אבל מייד יסטה ממנו. לכן יש הבדל מתמטי בין קווי אורך לקווי רוחב. מבחינה מתמטית, כל קווי האורך זהים זה לזה וכולם "ישר" – לעומת קווי הרוחב, שאינם "ישר". זאת אחת הסיבות העיקריות שעברו מאות שנים בין הצלחתם של בני האדם למדוד היטב קווי רוחב, ועד שהצליחו לעשות זאת עם קווי אורך: הרבה יותר קשה להבדיל בין קו אורך אחד לשני. יש ביניהם פחות הבדלים, ולכן לספינה בלב ים מסובך יותר לקבוע על איזה מבין כל קווי האורך הללו היא נמצאת עכשיו. ההבדלים הרבים יותר בין קווי הרוחב הקלו מאוד על ההתמצאות ביניהם.
עדיין לא מאמינים? מסלולי טיסה, שמתוכננים כמובן כך שיעברו בנתיב הקצר ביותר האפשרי בין שתי נקודות שנמצאות על אותו קו רוחב, לא משתרעים "ישר" ממזרח למערב לאורך קווי הרוחב, אלא עושים עיקול משונה צפונה (בחצי הכדור הצפוני). לעיתים המטוסים יצטרכו לטוס צפונה אפילו אם נקודת היעד שלהם נמצאת מדרום לנקודת המוצא! אבל העיקול הזה משונה רק אם בוחנים אותו על מפה שטוחה. על כדור, הקווים ה"מעוקלים" הללו הם פשוט... "ישרים". כלומר, חלקי מעגלים גדולים שעושים את הנתיב הקצר ביותר בין הנקודות. כי מתברר שללכת "ישר" על כדור זה לא פשוט כמו שזה נשמע.
7 צפייה בגלריה
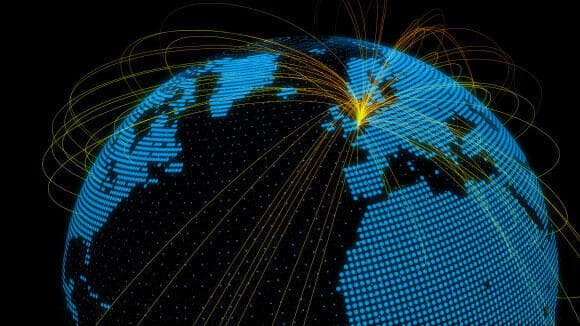

הקווים המעוקלים על המפה הם במציאות קווים ישרים. נתיבי טיסה על מפת העולם
(איור: shutterstock, עיבוד תמונה: מכון דוידסון)
מיכאל גורודין, מכון דוידסון לחינוך מדעי, הזרוע החינוכית של מכון ויצמן למדע