הזמן הוא תחילת המאה ה-17 והמהפכה המדעית כבר החלה, עם התגלית המרעישה שפרסם קופרניקוס ( Copernicus) כחצי מאה קודם, שכדור הארץ ושאר כוכבי הלכת מקיפים את השמש. קופרניקוס שיער כי המסלולים של כוכבי הלכת הם מעגלים מושלמים, אך יוהנס קפלר (Kepler) היה בטוח שקופרניקוס טועה לגבי צורת המסלולים, ושכוכבי הלכת אינם נעים במעגלים מושלמים.
לרשותו של קפלר עמדו מדידות מדויקות להפליא של תנועת מאדים בשמיים, שערך מורוֹ, האסטרונום טיכו ברהה (Brahe). בעזרת המדידות הללו, קפלר ניגש לחשב באופן ידני את מסלול התנועה של מאדים. אך החישוב התארך והלך, וקפלר טעה שוב ושוב. עברה שנה ועוד שנה, והוא אינו מצליח להגיע לתשובה. קפלר מתענה ומבקש עזרה מאסטרונומים אחרים. הם מסרבים, וקפלר ממשיך לבצע בעצמו את החישוב. ארבע שנים נדרשו לקפלר כדי להשלים את החישוב הזה, שאורכו כ-900 עמודים, ובמהלכן נאלץ לחזור עליו כ-70 פעמים! למזלו, קפלר לא ידע שחישוביו האחרונים היו רצופי טעויות, אשר בדרך נס ביטלו זו את זו כמעט לחלוטין.
המקרה של קפלר אינו יחיד. לאורך ההיסטוריה, הקושי בביצוע חישובים מורכבים הטריד מלומדים רבים ועיכב את התפתחות הידע האנושי. קושי זה הוליד מכשיר חישוב מהפכני: סרגל החישוב.
6 צפייה בגלריה


מהפכה בתחום החישובים המורכבים. המתמטיקאי הסקוטי ג'ון נפייר, שגילה את פונקציית הלוגריתם
(צילום: ויקיפדיה, נחלת הכלל)
הולדתו של סרגל הלוגריתמים
עם התקדמות המהפכה המדעית, התגבר הקושי בביצוע חישובים. חוקרים וטכנאים ביצעו מדידות מדעיות מדויקות, המתמטיקה התפתחה ומדענים נדרשו לבצע חישובים ארוכים ומורכבים. ואז קרה דבר מדהים. המתמטיקאי, הפיזיקאי והאסטרונום הסקוטי ג'ון נפייר (Napier) גילה פונקציה שהוא קרא לה "לוגריתם", שמאפשרת להפוך פעולות מסובכות של כפל וחילוק לפעולות פשוטות של חיבור וחיסור.
עוד כתבות באתר מכון דוידסון לחינוך מדעי:
עם מוח גדול באים חיים ארוכים
האנטיביוטיקה הנכונה לחולה הנכון
הפלישה הזוהרת
במונחים של היום, פונקציית לוגריתם בבסיס 10 של המספר x, אשר מסומנת log(x), מחשבת כמה פעמים צריך לכפול את 10 בעצמו כדי לקבל את המספר x. למשל, log(100)=2, כי 100 = 2^10, כלומר יש לכפול את 10 בעצמו פעמיים כדי לקבל את המספר 100. דוגמה לשימוש בלוגריתם היא כשאנחנו "סופרים אפסים" כדי לכפול את 100 ב-1,000: למעשה אנחנו מחשבים את הלוגריתמים שלהם בבסיס 10, log(100)=2 ו- log(1000)=3, ואז סוכמים אותם לקבלת 5 שהוא הלוגריתם של מכפלתם, 100,000. באופן כללי, ניתן לכתוב את הזהות הזאת כך: בעבור שני מספרים ממשיים, a ו-b מתקיים: log(ab)=log(a)+log(b).
6 צפייה בגלריה
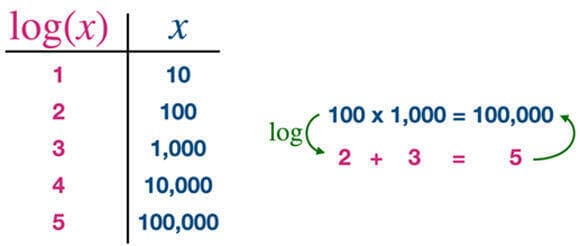
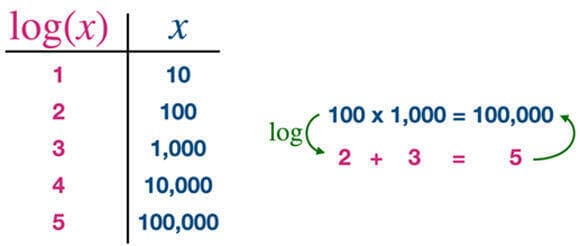
טבלאות לוגריתמים מאפשרות לחשב פעולות מסובכות של כפל וחילוק בעזרת חיבור וחיסור פשוטים
(איור: יובל רוזנברג)
בשנת 1614, לאחר כעשרים שנים של עבודה מאומצת, פרסם נפייר את תגליתו עם טבלה באורך 90 עמודים - לוח המפרט את הלוגריתמים של כעשרה מיליון מספרים. בלוח הלוגריתמים אִפשֵר למצוא את המכפלה של שני מספרים באופן הזה: יש למצוא בטבלה את הלוגריתם של כל אחד מהמספרים, לחבר בין שני הלוגריתמים שנמצאו ולבסוף למצוא את המספר שהלוגריתם שלו זהה לסכום שחושב - זוהי המכפלה הרצויה. כאשר אסטרונום ניגש לכפול שני ערכים של פונקציה טריגונומטרית, למשל 0.57357 ו- 0.42261, עליו למצוא בטבלה קירוב ללוגריתמים שלהם: (0.24141-) ו-(0.37406-), בהתאמה, לחבר שני מספרים אלו: (0.61547-), ולמצוא בטבלה את המספר שזהו הלוגריתם שלו: 0.242399. מספר זה הוא קירוב למכפלה המבוקשת. חיבור הוא פעולה פשוטה יותר מכפל, ולכן לוח הלוגריתמים הפך ללהיט, בעיקר בקרב אסטרונומים כמו קפלר, שההמצאה חסכה להם זמן וכוחות נפשיים רבים, ולכן הם אף שילבו לוחות כאלו בפרסומיהם.
בשנת 1620 פיתח המתמטיקאי והאסטרונום האנגלי אדמונד גנטר (Gunter) סרגל שאִפשֵר לחשב את המכפלה של שני מספרים על ידי מדידת אורכים, במקום להשתמש בטבלה שאורכה 90 עמודים. הסרגל נבנה כך שהמרחק מתחילתו אל מספר מסוים, x, הוא יחסי ל (log(x: הסרגל מתחיל במספר 1, שכן log(1)=0 ולכן המרחק אל 1 הוא 0, והמרחק בין המספר 1 לבין 3 הוא מחצית המרחק מהמספר 1 אל המספר 9, שכן log(3)=1/2log(9) . לחישוב המכפלה של המספרים a ו-b, יש למדוד את המרחק מתחילת הסרגל אל כל אחד מהמספרים הללו, ואז לסכום את שני האורכים (log(a)+log(b ולבדוק איזה מספר נמצא על הסרגל במרחק הזהה לסכום האורכים (log(ab.ס
ואז, בשנת 1622, לפני 400 שנים בדיוק, ויליאם אוטרד ( Oughtred) יצר את סרגל החישוב הראשון. היה זה כלי חישוב פשוט ונוח לשימוש, המורכב משני סרגלים לוגריתמיים זה לצד זה. כדי לחשב את מכפלת המספרים a ו-b, כל שיש לעשות הוא להסיט את הסרגל העליון כך שהמספר 1 יימצא מעל למספר a בסרגל התחתון, ולבדוק איזה מספר נמצא תחת המספר b. שם, במרחק log(ab)=log(a)+log(b) מתחילת הסרגל התחתון, כתובה המכפלה הרצויה: ab. ביצוע אותן הפעולות בסדר הפוך מאפשר גם לבצע חילוק, כיוון שחילוק הוא הפעולה ההפוכה לכפל. לצורך חילוק המספר ab ב-b, יש להציב את המספר b בסרגל העליון מעל המספר ab בסרגל התחתון, ולקרוא את המספר שנמצא מתחת למספר 1 שבסרגל העליון.
6 צפייה בגלריה
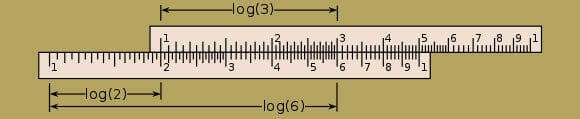

מהפכת החישוב המהיר. חישוב מכפלת המספרים 2 ו-3 בעזרת סרגל חישוב בסיסי
(איור: Jakob.scholbach, Wikipedia)
350 שנות חישוב
המצאת סרגל החישוב הקלה מאוד את ביצוע פעולות הכפל והחילוק. החלו להשתמש בו מתמטיקאים, מדענים, מהנדסים, רופאים, גיאוגרפים, אנשי צבא, טייסים, פקידי מס ועוד. אייזק ניוטון, תומס ג'פרסון, אלברט איינשטיין, כולם השתמשו בסרגל חישוב. הוא סייע כמעט בכל המצאה, בכל תכנון של מבנה היסטורי, בכל פיתוח מדעי משמעותי, במשך כ-350 שנים.
ככל שהשימוש בו נעשה נרחב יותר, כך סרגל החישוב הלך והשתכלל. לצד הסקלות הלוגריתמיות ה"רגילות", החלו להופיע סקלות נוספות שאפשרו לחשב פונקציות רבות, כמו סינוס, שורש, ריבוע ואקספוננט. למשל, לחישוב ריבוע ושורש ריבועי, נוצרה סקלה לוגריתמית שבה המספר x^2 מופיע מעל כל מספר x בסקלה הרגילה: מעל המספר 1 מופיע 1, מעל 2 מופיע 4, מעל 3 מופיע 9 וכן הלאה. קריאת מספרים המופיעים זה מעל זה באותו המרחק מתחילת הסרגל, אך בסקלות שונות, היא כל מה שנדרש לחישוב הפונקציה, הריבוע או השורש בדוגמה זו. הוספת קו דקיק אנכי, הניתן להזזה לאורך הסרגל, הקלה על השוואת המספרים בין הסקלות, ואפשרה לחשב את הפונקציות בדיוק של שלוש ספרות. כתיבה מדעית אפשרה לבצע את החישובים בעבור כל מספר, גדול או קטן.
6 צפייה בגלריה


המכשיר הלך והשתכלל. סרגל חישוב עם סקלות שונות, הקו הדקיק שאפשר להזיז לאורך הסרגל מאפשר קריאה נוחה ומדויקת של תוצאות החישוב
(צילום: shutterstock)
נוסף על חישוב פונקציות כלליות, היו גם סרגלים ייעודיים, בעלי סקלות שתוכננו לסייע בחישובים מסוימים. אלו כללו המרות בין יחידות שונות, חישובי הלוואות בנקאיות, חישובים הנדסיים ומחשבי טיסה שלמים ששימשו לביצוע חישובים הקשורים לטיסה. היו גם סרגלים מעגליים, ואף גליליים.
6 צפייה בגלריה


מכונאי מוטס במפציץ בריטי נעזר בסרגל חישוב כדי לחשב את צריכת הדלק של המטוס, אוקטובר 1941
(צילום: Royal Air Force, Public Domain )
סרגל החישוב נחשב במשך זמן רב לשיא הטכנולוגיה, ונותר רלוונטי גם עם המצאת שלל אמצעי חישוב מכניים אחרים. אך הסרגל התקשה להתחרות במחשב הדיגיטלי, ובעיקר בגרסה הממוזערת שלו. מאמר משנת 1972 בישר על מכת המחץ שייתרה בן לילה את השימוש בסרגל: "כאשר מהנדס או מדען נדרש לחישוב מהיר של בעיה הדורשת כפל, חילוק או פונקציה טרנסצנדנטלית, הוא ניגש בדרך כלל לסרגל החישוב שנמצא תמיד בהישג יד. אך בתוך זמן קצר, הכלי הזה עשוי לצאת לגמלאות. כעת יש מחשבון כיס אלקטרוני אשר מספק את אותן התוצאות בקלות רבה יותר, מהר יותר ובאופן מדויק הרבה יותר". בכך המחשב עשה את הלא ייאמן, וסיים פרק חשוב בהיסטוריה של המדע ושל המין האנושי כולו – עידן שלם שהתבסס על כלי חישוב פשוט להפליא.
6 צפייה בגלריה


סוף עידן הסרגל: מחשב אחד יכול להחליף 150 מהנדסים (עם סרגלי חישוב). מודעת פרסומת של חברת IBM למחשב שלה משנת 1951
(צילום: ויקיפדיה, נחלת הכלל)
ד"ר יובל רוזנברג, מכון דוידסון לחינוך מדעי, הזרוע החינוכית של מכון ויצמן למדע

