גם כיום, כ-200 שנה מאז הולדת הכימיה האורגנית, חוקרים ברחבי העולם ממשיכים לחפש דרכים להפיק תגובות כימיות יעילות יותר. רק לפני קצת יותר משנה זכו בפרס נובל לכימיה קרוליין ברטוצי (Bertozzi), מורטון מלדל (Meldal) וקרל בארי שרפלס (Sharpless) על פיתוחה של הכימיה בקליק, שמחברת היטב זו לזו מולקולות שלא בהכרח קל לחברן בשיטות מסורתיות.
המבנה המרחבי והגיאומטרי של מולקולות משפיע מאוד על היכולת שלהן להשתתף בתגובות כימיות. מבנים גיאומטריים מסוימים יכולים לחסום אתרי תגובה, כלומר אזורים פעילים במולקולות שאליהם יכולות להתחבר מולקולות אחרות, או ליצור אתרי תגובה חדשים. אם כן, אין פלא שכימאים רבים מתעמקים בתיאוריות גיאומטריות מורכבות ובענפים אחרים של המתמטיקה העוסקים בצורות של גופים.
3 צפייה בגלריה


זוכי פרס נובל קרוליין ברטוצי (Bertozzi), מורטון מלדל (Meldal) וקרל בארי שרפלס (Sharpless)
(צילום: AFP)
אחד מענפי המתמטיקה המעניינים בהקשר הזה הוא תורת הקשרים (Knot theory), ששואפת לאפיין ולמיין קשרים מבחינה מתמטית. לענייננו, אפשר להתייחס לקשר כאל חבל שפיתלנו סביב עצמו ואז הדבקנו את קצותיו יחד ויצרנו תבנית סגורה שחוצה את עצמה כמה פעמים. במקרה שלנו החבלים הם מולקולות, והקשרים הם אובייקט מתמטי גרידא. לא נדבר כאן על קשרים כימיים במובן הרגיל, כמו קשר מימן או קשר קוולנטי, שהם חיבורים מקומיים בין אטומים, אלא על קשרים במובן הגיאומטרי.
לאחרונה התפרסם בכתב העת Nature Communications מאמר שהציג שיא חדש ביצירת מולקולה קשורה (ולא טריוויאלית) קצרה והדוקה במיוחד - המונה 54 אטומים בלבד. ציינו "לא טריוויאלית" מכיוון שבטבע יש המון מולקולות קצרות מאוד, למשל מימן מולקולרי המונה שני אטומים בלבד. הכוונה כאן היא למולקולות שצורתן מזכירה עלי תלתן. קשר תלתן הוא הקשר הפשוט ביותר שאינו מעגל. בעוד מעגל אינו חוצה את עצמו כלל, תלתן חוצה את עצמו שלוש פעמים, וזה המספר המזערי האפשרי של חיתוכים.
מולקולות קשורות הן תופעה שכיחה למדי בטבע. הקצרות והטריוויאליות שבהן הן טבעות פשוטות. למשל בנזן היא מולקולה של שישה אטומי פחמן המחוברים זה לזה. יש גם טבעות הרבה יותר ארוכות, אך עדיין קצרות במהותן, כגון מולקולת ה-DNA, שנוטות להיקשר באופן טבעתי במערכות ביולוגיות כמו התא החי. ה-DNA המיטוכונדרי, למשל, קיים בצורת טבעת. אותו דבר נכון גם למולקולות RNA ולחלק מהחלבונים. לכן ברור מדוע חקר מולקולות קשורות וקצרות יכול לשפוך אור על מנגנונים ביולוגיים וביוכימיים, וגם על חלק מהפולימרים ומסוגי הפלסטיק.
כימיה של קשרים
ב-1989 התפרסם לראשונה מאמר שהציג תהליך כימי של קשירת מולקולה לצורת תלתן. בהמשך התברר שגם DNA טבעתי אפשר לשנות לקשר דמוי תלתן. בשלושת העשורים האחרונים נערכת תחרות לא רשמית בין חוקרים על בניית הקשרים הקצרים ביותר, בשאיפה לגרד את הגבול הנמוך ביותר האפשרי. כדי לכמת את ההישגים הוגדר מדד בשם "יחס חציית השלד" (Backbone Crossing Ratio, או BCR), שמבטא את היחס בין מספר האטומים במולקולה הקשורה לבין מספר הצמתים בקשר. לדוגמה, יחס חציית השלד של מולקולה דמוית תלתן המורכבת מ-99 אטומים יהיה 33, מכיוון שבתלתן יש שלושה צמתים. ואכן, לרוב קשרי התלתן שנוצרו עד לשנים האחרונות היה BCR בין 27 ל-33.
3 צפייה בגלריה
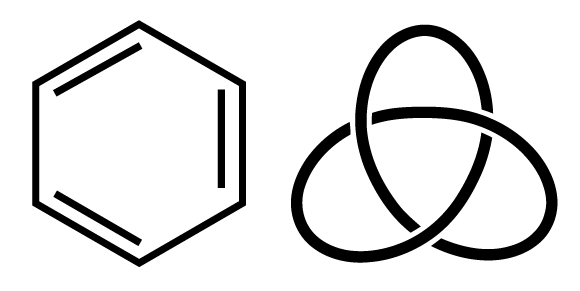

מולקולת בנזן (שמאל) היא טבעת פשוטה המורכבת משישה אטומי פחמן קשורים זה לזה, קשר תלתן (ימין) הוא הקשר הפשוט ביותר שאינו מעגל
(איור: Kicky_princess; igor kisselev, Shutterstock)
ב-2020 יצרו כימאים מסין מולקולה דמוית תלתן שבה 69 אטומים, דהיינו BCR של 23. לצורך התגובה הכימית הם השתמשו באטומי מתכת, ואחרי שסילקו אותם בסופה נותר מבנה תלתן יציב ובלי ניתן לשבירה. זה היה הישג מרשים, אך כעת גם השיא הזה נשבר. המאמר החדש מציג מולקולה דמוית תלתן שבה 54 אטומים, כלומר ה-BCR שלה הוא 18 בלבד.
קשרים הדוקים
ככל שמולקולות קשורות הן קצרות יותר, הקשר חזק יותר: המולקולה פשוט מאבדת את גמישותה. התופעה תואמת היטב גם את הציפיות שלנו מחיי היומיום - למשל חבל קצר הוא פחות גמיש מחבל ארוך מאותו סוג. חישובים קוונטיים שבחנו את הגבול התחתון האפשרי לגודלן של מולקולות דמויות תלתן, וגילו כי הוא עומד על כחמישים אטומים. אם ההערכה הזאת אכן מדויקת, הרי שנותר עוד מעט מאוד מקום למזעור נוסף של קשרי תלתן מולקולריים.
כמו לא מעט תגליות, גם כאן יד המקרה מילאה תפקיד מרכזי. הכותב הראשי של המאמר, ריצ'רד פדפאט (Puddephatt) מאוניברסיטת מערב אונטריו, סיפר כי הוא ועמיתיו ניסו בכלל ליצור מולקולות של אצטלידים, שיש להן שימושים רבים בתגובות בכימיה אורגנית. כשחיברו אצטיליד זהב למבנה שנקרא דו-פוספין (diphosphine), נוצר במקרה המבנה התלתני, במקום שרשרת של אטומי זהב שהם ציפו לקבל. גם זה לבדו חידוש: הקשר נוצר באופן ספונטני, בהרכבה עצמית. החוקרים מודים שהם לא מבינים את התהליך הכימי שהתרחש כאן, אך אין ספק שהוא יתברר בשנים הבאות, ואפשר לצפות שהקשרים ההדוקים יזכו ליישומים רבים.
אמנות האפשר
התגלית החדשה הייתה משמחת בוודאי את האמן ההולנדי מאוריץ קורנליס אשר (Escher), שהיה חובב מושבע של גיאומטריה. התחריט "קשרים" שלו הציג בדיוק את הקשרים דמויי התלתן הללו.
נוסף על התלתן יש כמובן עוד סוגים רבים של קשרים בעלי תכונות מעניינות. חלקם מקוטלגים בשפה מתמטית שנקראת "כתיב אלכסנדר-בריגס" (Alexander-Briggs), שמצמיד לכל קשר שני מספרים. הראשי מביניהם מונה את הצמתים בקשר, ואילו המספר המשני הוא מדד שרירותי שמבדיל בין סוגי קשרים בעלי אותה כמות צמתים. למשל התלתן מקוטלג בתור 31. עם זאת, אין כיום אלגוריתם שיכול למיין את כל הקשרים, כלומר כלל שיוכל לקבוע עבור כל שני קשרים אם הם שתי הצגות שונות של אותו קשר או קשרים שונים.
יהונתן ברקהיים, מכון דוידסון לחינוך מדעי, הזרוע החינוכית של מכון ויצמן למדע


