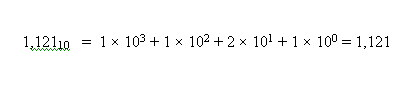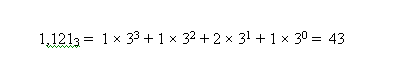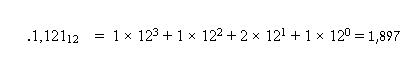האם ביטול השיטה העשרונית הוא רעיון מופרך?

(מספר ללא סימון הבסיס, כמו המספר 1,121 שבתוצאה, מציין את הכמות לפי בסיס 10.)

בבסיס אחר, המחוברים הם מכפלות של הספרות בחזקה המתאימה של הבסיס. אם מופיע המספר 1,121 בבסיס 3, ערכו שווה למה שהיינו מציינים בבסיס 10 כ-43:

ובבסיס 12 המספר 1,121 שווה למה שהיינו מציינים בבסיס 10 כ-1,897:

כאמור, הארגון הדוזנאלי הציע לעבור לשיטה המבוססת על בסיס 12. בשיטת הספירה המוצעת, במקום עשר ספרות יהיו שתים-עשרה ספרות, כאשר יוקצו סימנים עבור המספרים עשר ואחת עשרה, למשל: χ = 10, є=11. המספר 22 בבסיס זה ייכתב כך:

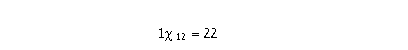
חברי הארגון מספקים שלל נימוקים, חלקם אפילו משכנעים למדי, מדוע מהלך כזה היה מקל את חיי היומיום. בין השאר,

משבחים חברי הארגון את המספר 12 משום שהוא מתחלק בשלמות ל-2, 3, 4, ו-6, בניגוד למספר 10, המתחלק רק ב-2 וב-5. הם גם מציינים שהשימוש במספר שתים-עשרה כיחידת מנייה של משהו שלם עדיין נפוץ למדי, בעיקר במדידות של זמנים: ישנם 12 חודשים בשנה ו-12 שעות ביום. ישנן 360 זוויות במעגל, שהן שלושים פעמים 12, מעין "פשרה" בין השיטה העשרונית לשיטה הדוזנאלית.

ניתן לראות בבירור את היתרון במקרה זה אם משווים בין מעגל המחולק ל-12 זוויות לבין מעגל המחולק ל-10 זוויות. כשמעגל מחולק ל-10 זוויות, הזוויות של רבע, שליש ושישית מעגל הן כולם שברים, בעוד שבמעגל המחולק ל-12, זוויות אלה הן מספרים שלמים. בעבר, בחלק מהתרבויות, מידות פיזיקליות שונות (כמו אורך ומשקל) היו מבוססות על בסיס 12 דווקא, ועד היום אפשר לקנות ביצים בתבניות של 12. הקמיע של הארגון, אגב, הוא דוב הפנדה, בשל העובדה שיש לו שש אצבעות בכל כף יד.

גם אם אנחנו לא ממש משתכנעים מהנימוקים של הארגון הדוזנאלי, עדיין ראוי להגות מעט ברעיון המציע להשתמש בבסיס הנוח ביותר לשם החישוב הספציפי שאותו אנחנו רוצים לבצע.

רעיון זה מבוצע הלכה למעשה במחשב, שבו כל הפעולות מבוצעות בשיטה הבינארית – בבסיס 2. באותו אופן, ישנם שימושים גם לבסיס הטֶרנארי (בסיס 3). בין השאר, נבדק הרעיון לבנות מחשב לפי בסיס שלוש, שבו ייעשה שימוש בשלושה מצבים שונים של המעגלים החשמליים הפנימיים: מצב של זרם חיובי (זרם בכיוון אחד), מצב של זרם שלילי (זרם בכיוון האחר) ומצב שבו אין זרם כלל. לשיטה זו יתרונות רבים. במחשבים ובאלקטרוניקה נעשה שימוש גם בבסיס האוֹקטאלי (בסיס 8) ובבסיס ההֶקסאדֶצימאלי (בסיס 16).

גם אליס ספרה אחרת

לא רק מתמטיקאים השתעשעו בבסיסים. ישנם גם סופרים ידועים שהרהרו באפשרות של שיטות ספירה נוספות, ביניהם הסופר המפורסם והמצוין ג'.ר.ר. טולקין, שכתב את טרילוגיית "שר הטבעות". טולקין המציא לצורך ספריו שפות חדשות עבור האֶלפים ("בני הלילית"). אחת מהשפות האלה מכונה "שפת הקווניה", ושיטת הספירה שהמציא טולקין לדוברי שפה זו היא לפי בסיס 12.

סופר ידוע נוסף שהשתעשע בבסיסים היה לואיס קרול, מחבר "אליס בארץ הפלאות". בספר "אליס בארץ הפלאות" אליס בודקת את שפיותה לאחר נפילתה לתוך ארץ הפלאות: "אנסה לבדוק אם אני יודעת את כל הדברים שידעתי פעם. רגע אחד: ארבע כפול חמש הם שתים-עשרה, וארבע כפול שש הם שלוש-עשרה, וארבע כפול שבע הם – אוי ואבוי! בקצב כזה לעולם לא אגיע עד עשרים!". מתמטיקאים שיערו שקרול בעצם מתייחס כאן לסדרה של תרגילי חשבון בבסיסים שונים, עם חוקיות מסוימת. סדרת התרגילים היא:

4 × 5 = 12 בבסיס 18.

4 × 6 = 13 בבסיס 21.

4 × 7 = 14 בבסיס 24.

4 × 8 = 15 בבסיס 27.

4 × 9 = 16 בבסיס 30.

4 × (10) = 17 בבסיס 33.

4 × (11) = 18 בבסיס 36.

4 × (12) = 19 בבסיס 39.

(הערה: המספרים המסומנים בסוגריים הם ספרות יחידות בבסיסים גבוהים.)

שימו לב לחוקיות המעניינת, בבסיסים (הגדלים בשלוש בכל תרגיל), בכופלים ובתוצאות של התרגילים. לפי חוקיות זו, התשובה לשאלה: באיזה בסיס 4 × (13) = 20 אמורה להיות בסיס 42, אבל מסתבר שתשובה זו איננה נכונה! זאת הסיבה שאליס לעולם לא תגיע עד עשרים.

ככל שמתמטיקאים התעמקו בבסיסים, הם גילו עולם מתמטי מרתק. בין השאר, ההגדרה של בסיס הורחבה לכלול גם בסיסים שליליים, בסיסים שבורים ובסיסים נוספים, כמו בסיס עצרת ובסיס ראשוני, ששניהם אינם חזקות של מספרים שלמים. כך שבין שאתם מצדדים בהצעתו של הארגון הדוזנאלי ובין שאינה נראית בעיניכם, העיסוק במתמטיקה בבסיסים שונים מבטיח לכם שעות רבות של הנאה מתמטית.

פורסם במקור במגזין "גלילאו "