איך להשתמש נכון במודלים מתמטיים לקורונה
מהם מודלים? איך הם מצליחים לנבא את העתיד? עד כמה הם עלולים לטעות? ואיך אם כן, כדאי להשתמש בהם?
עוד אחד מהדברים שפרצו לחיינו יחד עם נגיף הקורונה הוא המודלים המתמטיים. בעצם, הם נמצאים סביבנו כל הזמן - במזג אוויר, בפרסומות ממוקדות, או עזרי ניווט - אך לרוב איננו מודעים לקיומם.
המודלים הופיעו לנגד עינינו עם התפרצות הקורונה כשניסינו לחזות באמצעותם את מהלך המחלה החדשה, ואת השפעתם של צעדים חברתיים שונים. מושגים כגון "גדילה מעריכית" ״השטחת העקומה״ ו"ריחוק חברתי" נעשו לפתע שגורים בפי כל. גם כעת הם עדיין איתנו, משתדלים לנבא מהן ההשפעות האפשריות של ההקלות השונות על מהלך המחלה, לנחש האם/מתי יהיה "גל שני" ובאיזו עוצמה, ולניהול שוטף של אירועים מתגלגלים.
מומחים משדות מדעיים שונים מציגים את המודלים ואת תוצאותיהם, שלעתים נושאות יכולת ניבוי טובה ולעתים פחות. והקורא או השומע נשאר תוהה, האם להאמין לזה שנשמע ממש צודק, או לזו שנראית ממש אמינה? להביע דעה נחרצת אין בידינו, אך נשתדל לענות על כמה שאלות: מהם מודלים? איך הם מצליחים לנבא את העתיד? עד כמה הם עלולים לטעות? ואיך אם כן, כדאי להשתמש בהם?
מהו מודל?
באופן הפשוט ביותר, מודל הוא דגם של העולם. על מנת לתפוש תופעה אנו מפשטים אותה וכך משתדלים להבין את המתרחש בעולם. כולנו משתמשים במודלים, כל הזמן. המוח שלנו הוא מוכוון עתיד, צופה כל הזמן מה יקרה ומייצר תחזיות כדי שנצליח, או במונחים אבולוציוניים, נשרוד.
אחת התחזיות שכולנו מסתמכים עליהן היא תחזית מזג האוויר. תחזית זו היא די אמינה לטווח הקצר, ומבוססת על מודל מורכב כדי לחזות טמפרטורה, רוחות וגשמים. לעניין הקורונה, אנו רוצים לדעת איך וכמה מהר מתפשט נגיף הקורונה, מה הסיכוי לתחלואה ותמותה, מה ההשלכות בהינתן האופי של מדינת ישראל (למשל גורמים מקטיני סיכון כמו מדינה סגורת גבולות, ומגבירי סיכון כדוגמת יחסים קרובים בין דורות שונים במשפחה), ומה המשמעות של הטלת צעדי מניעה אפשריים והסרתם (כמו ריחוק חברתי, סגירת/פתיחת בתי ספר).
מהו מודל מתמטי?
מודל מתמטי משתמש בשפת המתמטיקה כדי לתאר תופעה בעולם הטבע או החברה. למה זה טוב? מכיוון שהטבע משום מה מדבר בשפת המתמטיקה. מתמטיקה היא קודם כל שפה, וכמו כל שפה אחרת, היא מאפשרת לקרוא לעצמים בשמות, ולבנות משפטים וקשרים. היתרון של המתמטיקה על שפות מדוברות כמו עברית, ערבית ואנגלית הוא שהיא מאפשרת לנו לפשט מערכת מורכבת למרכיביה הבסיסיים, ואז להשתמש בכלים מתמטיים כגון משוואות במספר נעלמים כדי לחזות איך המערכת תתפתח בעתיד, ואיך היא תגיב לשינויים. מודל טוב מפשט את העולם ומפריד בין עיקר וטפל, מתאר רכיבים וקשרים ביניהם בצורה פשוטה, אך לא פשוטה מדי. צורה שעדיין מאפשרת לנו להבין, ללמוד ולצפות שינויים במערכות מורכבות.
אחד המודלים המתמטיים הפשוטים התגלה כבר בשנת 1202. הוא נקרא "סדרת פיבונאצ'י" וכולל את רצף המספרים ...1,1,2,3,5,8,13. המתמטיקאי האיטלקי לאונרדו פיבונאצ'י גילה את הסדרה הזו כאשר ניסה לחשב ריבוי טבעי של ארנבים.
פיבונאצ'י הניח מספר הנחות לא מציאותיות: כל ארנבת מולידה זוג ארנבים, ארנב וארנבת, וכל זוג מתחיל לאחר חודש להוליד זוג חדש, אחד בכל חודש. תחת הנחות אלו פיבונאצ'י הראה שמספר זוגות הארנבים בחודש N יהיה שווה לסכום המספרים בחודשים 1-N ו-2-N.
המודל של פיבונאצ'י רחוק מאוד מחייהם של ארנבים אמיתיים, אבל תחזית אחת שלו מתאימה למציאות: אוכלוסייה של אורגניזמים, בין אם הם ארנבים, בני אדם או וירוסים, לרוב תתרבה בצורה מעריכית (אקספוננציאלית) כל זמן שיש לה מספיק משאבים ואין לה אויב טבעי.
במקרה של נגיף הקורונה, המשאב של הנגיף הוא החומר הגנטי שלנו, והאויב הטבעי שלו הוא מערכת החיסון שלנו. כל זמן שלווירוס יש גישה לבני אדם רבים שטרם נחשפו אליו בעבר, ובהנחה (לא מוכחת עדיין - אפשר שיש השפעה, אולי גנטית, על חסינות טבעית) שלאנשים אלו אין נוגדנים כנגדו, הוא ימשיך להתרבות אקספוננציאלית. מודלים יכולים לסייע לנו להגיע לתובנות שהן לא אינטואיטיביות, למשל בהתפשטות מחלות - האינטואיציה האנושית לא מסוגלת לתפוש שאם היום יש עשרה חולים ולא נעשה דבר, בתוך חודשיים שירותי הרפואה יקרסו מרוב עומס. המתמטיקה אינה כבולה לאינטואיציה שלנו ולכן יכולה לגלות לנו אפשרויות סבירות עתידיות.
איך מודלים מפיקים תחזיות?
מודלים מצליחים להפיק תחזיות טובות כתוצאה משילוב הרעיון הבסיסי שביסודם (למשל בסדרת פיבונאצ׳י גדילה מעריכית), עם נתונים נכונים על העולם (ארנבים אינם מולידים בהכרח זוגות על בסיס חודשי). בהקשר של התפשטות הקורונה, יש שני סוגי מודלים אפידמיולוגיים עיקריים: מודלים סטטיסטיים (מבוססים על התאמת תבניות לנתונים) ומודלים מכניסטיים (מתבססים על הבנת התהליך).
המודל הסטטיסטי "מחפש" קו (או: עקומה) המתאים ביותר לנתונים שהצטברו עד הרגע הנוכחי (למשל, מספר החולים הקשים לאורך הזמן). הקו מתאפיין בתבנית מתמטית מסוימת, והמשכו של הקו אמור לנבא את העתיד (למשל, מספר החולים הקשים כעבור פרק זמן נוסף). אנחנו בעצם מנסים להבין האם יש תבנית שניתן לזהות במידע. היתרון של מודל כזה הוא שהמודל אינו דורש הרבה ידע או הנחות מוקדמות (יתרון משמעותי בעניין וירוס הקורונה שאינו מוכר למדע עדיין). הצד השני של המטבע הוא שניתן להתחשב בניבויים שלו רק לטווחי זמן קצרים יחסית. מעבר לטווחים הללו עלולים לבוא לידי ביטוי אפקטים מורכבים שיכולים לשנות את התמונה.
מודל מכניסטי לעומת זאת, מנסה להבין את מהלך המחלה. הוא מנסה לתאר את תהליכי ההדבקה עצמם, שתלויים במבנה האוכלוסייה והתהליך (ההסתברותי) שעובר כל אדם מרגע שהוא נחשף לחולה פוטנציאלי. אחד המודלים הפופולריים בקטגוריה הזו נקרא מודל SIR (ראשי תיבות של Susceptible-Infected-Recovered, המצבים האפשריים שאדם עובר מרגע החשיפה לווירוס). אחת הבעיות של מודלים כמו SIR היא שאנחנו לא בהכרח מבינים לעומק את התהליך הבסיסי או שאין לנו הערכה טובה מספיק של הפרמטרים שנכנסים למודל, וגם עם הרחבות אפשריות (למשל הוספת מצבי ביניים, פרמטרים שונים של הדבקה, נתונים על התקדמות המחלה בקבוצות שונות באוכלוסייה), עדיין עלולים להימצא אי דיוקים משמעותיים.
למה מודלים אינם מדויקים?
הסיבה הראשונה קשורה לידע החלקי הקיים בדבר נתוני-עולם הכלולים במודל. בהקשר למחלת הקורונה, נכנסים למודל נתונים רבים מאוד. חלק נוגעים למאפיינים של המדינה הממודלת (התפלגות הגילאים, איכות מערכת הבריאות, בריאות האוכלוסייה) או לאופי הקשרים במדינה (למשל: כמה אנשים פוגש כל אחד במדינה מכל שכבת גיל, צפיפות אוכלוסין, ציות להוראות בקהילות שונות). חלקם נוגעים לביולוגיה של הווירוס עצמו (למשל: תת זנים של הווירוס והיחסים ביניהם, תלות בטמפרטורה ובלחות) או לביולוגיה של הנשאים (למשל נשאים המבטאים את הוירוס ביתר ומפיצים אותו יותר, שכבות גיל שנדבקות יותר ושכבות שמדבקות יותר).
על כן אנו צריכים להקיש ממידע ידוע, לנחש על סמך נתונים דומים או "לשערך פרמטרים". הניסיון שלנו עם מחלת הקורונה ועם המחולל הוא מצומצם ועל כן שיערוכים תופסים מקום רב משהיינו רוצים. ככל שהפרמטר המשוערך משפיע יותר על המודל, המודל חשוף יותר לטעות (או פחות "יציב"). סיבה אחרת היא ה"משקל" שמקבלים הנתונים הללו. אנו יכולים לכוונן את השפעתם של פרמטרים שונים על המודל על מנת שיתאימו לתוצאות, ולטייב את תוצאות המודל עם הזמן, אבל ההתערבות הזו תלויה בתוצאות האמת, וככל שאנו נמצאים בשלב יותר התחלתי התוצאות פחות מדויקות, ולא ברור איך ניתן להשליך ממקום אחד על מקום אחר (תמותה בצפון איטליה לעומת אוסטריה הסמוכה לה, לדוגמה).
ולבסוף - ישנה גם אקראיות המובנית בבעיה שעמה אנו מתמודדים. כמו האפשרות שבראשית ההתפרצות יהיה משחק כדורגל חשוב ועיר ומלואה יצטופפו בו (ע״ע ברגמו, איטליה), או שאדם מסוים גם יהיה "מפיץ על" ביולוגי וגם ייחשף להמוני אנשים. כן, כמו שלפעמים המזל משחק לטובתנו, לפעמים גם הרעים שולפים בלאק ג'ק.
אז איך מודל יכול לחזות משהו באופן מדויק?
לבעיות מורכבות הרבה פעמים אין תשובות פשוטות. למשל, טענה שנשמעה בעבר כי "בישראל נגיע ל-97% (מיגור הקורונה) ב-5 מאי, 99% ב-17 במאי ומיגור סופי ב-9 ביולי", אינה מחזיקה מים.
במתמטיקה ובסטטיסטיקה פותחו הרבה כלים שמאפשרים להתמודד עם חוסר דיוק המובנה במודל או שנובע מאי דיוק בפרמטרים המוזנים אליו. מדד פיזור, כמו למשל סטיית תקן, מספר לנו עד כמה התחזיות השונות רחוקות זו מזו. רווח סמך (או בת זוגו, רמת המובהקות) מציינים עד כמה יכולת ההסקה ממדגם נתון מדויקת.
טווח שגיאה אפשרי מאפשר לנו להחליט עד כמה לסמוך על התחזית שהמודל נותן. חשוב להבין שהנתונים הללו על אודות המודל חשובים לא פחות מן התוצאה עצמה על מנת שנדע להעריך את משמעות התוצאה ולהשתמש בה לאור הסיכונים שבתוצאה מחד והסיכויים שהיא מציעה מאידך.
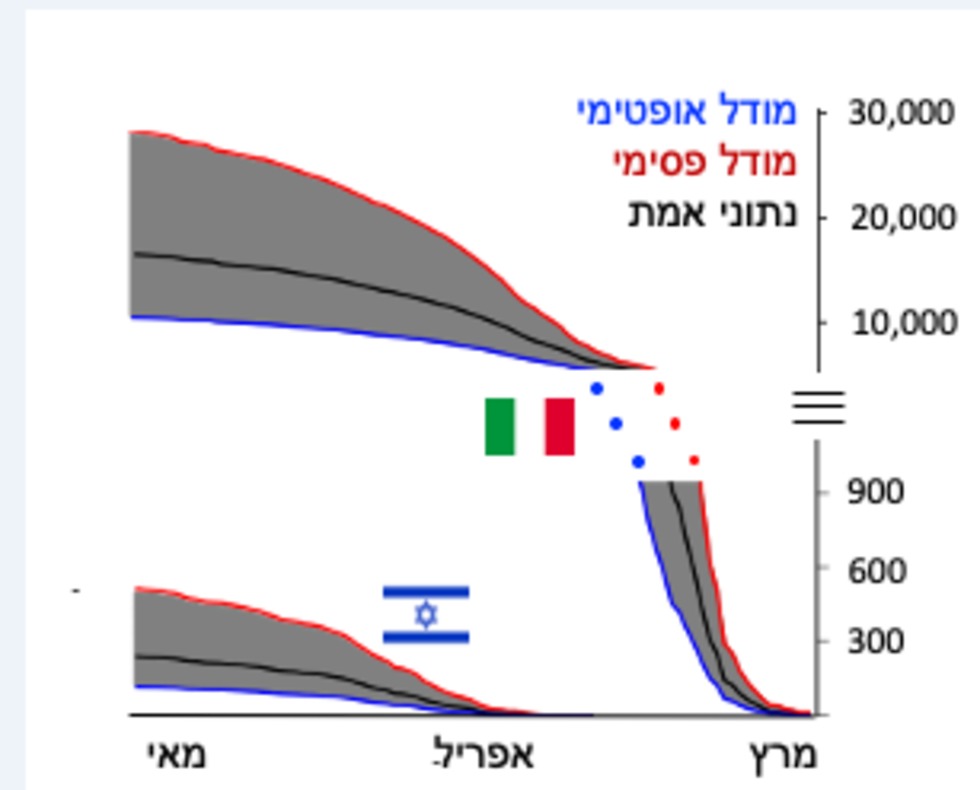
בתמונה משמאל ולמטה ניתן לראות הדמיה של מודל שאנו מריצים על אוכלוסיית ישראל (כלומר לפי פרמטרים מתאימים לתנאים במדינת ישראל) ועל חבל לומברדי שבאיטליה (למעלה ומימין) המתאר את התמותה מקורונה (מספר הנפטרים) לאורך הזמן. הקו האדום הוא "מודל פסימי", כלומר הפרמטרים שנכנסים למודל יובילו לתוצאות קטלניות יותר והכחול - אופטימי. באפור נמצא טווח הביניים. נתוני האמת, לרוב, יהיו איפשהו באמצע, כמו שאכן מתאר הקו השחור.
אז איך אפשר לעשות ככה מדע?
הפוך, גוטה,הפוך. רק כך אפשר לעשות מדע. במקרים שבהם אין לנו מספיק מידע, ויש אי וודאות שנובעת ממקורות שונים (כמו שינויי מדיניות והמורכבות של ההתנהגות האנושית) נרצה להתחשב באי הוודאות ולהתמודד עימה, ובטח שלא להתעלם ממנה. נעדיף להסתמך על טווח סביר של תוצאות אפשריות, ולהיערך גם למקרי קצה.
במובן יותר כללי, אחד המסרים המשמעותיים של התאוריה המדעית הוא הטלת הספק המושרשת במדע. טענה מפורסמת של פילוסוף המדע קרל פופר היא שתאוריה מדעית שאינה ניתנת להפרכה או לסתירה אינה נחשבת תאוריה מדעית. ובאמת, הבניין המדעי נבנה בתהליך של "רצוא ושוב" שהופכים אותו ליותר ויותר מדויק.
ב-1514 הבין קופרניקוס שכדור הארץ סב סביב השמש ולא להיפך, ב-1687 גילה ניוטון שיש כבידה (גרוויטציה) וחוקי תנועה, וב-1915 דייק אינשטיין את המערכת מתוך הבנות לא טריוויאליות על אודות מרחבים עקומים, מערכות מואצות או העובדה שגוף אינו יכול לנוע במהירות הגבוהה ממהירות האור. הבחינה המתמדת והמחודשת של ההנחות, השיטות, התוצאות והמסקנות המדעיות; המודעות למגבלות; החתירה לשקיפות מלאה ולביקורת מתמדת הן מאבני היסוד של החשיבה המדעית, והמדע חב להן את הצלחתו. אנו, החוקרים, מישירים עיניים אל המדע ואז משפילים אותן כי לא הצלחנו לדייק, כי לא גילינו את כל התמונה, ממשיכים לחפש - ומנסים שוב. כך, לדעתנו, יש לפעול גם במידול מגפת הקורונה.
אבל אנו צריכים להגיע למסקנות כעת, לא בעוד שנים של מחקר מדעי?
נכון. ולמרות אי הוודאות שהמדע מקדש הוא הצליח להביא אותנו לשיאים יישומיים במהירות פנטסטית (למשל טכנולוגיה דיגיטלית). אבל לשם כך צריך להבין היטב את המודלים, את הנתונים, את התחזיות, ואת אפשרויות הטעות, ורק אז להסיק מסקנות מעשיות. למרבה השמחה, זה בדיוק מה שמדענים יודעים לעשות - להתמודד עם אי וודאויות ועם טעויות הניבוי של המודל.
לגבי הראשונה, דרך התמודדות היא להוציא מספר ניבויים (פרדיקציות) אפשריים ולהציג טווח אפשרי ולא תוצאה אחת בלבד. בנוסף, אנו מטייבים את המודלים באופן תמידי, מחשבים ומניחים "חסמים" על הנתונים שמוזנים למודלים כדי לוודא שגם אם ישנה טעות הרי שהיא בגדר הסביר.
עם הזמן והצטברות הנתונים ניתן לדייק יותר ויותר. הגרף התחתון בתמונה הוא המודל מכוונן למדינת ישראל, שלה גבולות סגורים, נסועה מצומצמת, מעט "מפיצי-על", ובה גם הוטלו צעדים משמעותיים ביותר לאורך הזמן.
בחלק הימני והעליון של התמונה אפשר לראות את המודל לגבי חבל לומברדי שבאיטליה (שימו לב לעלייה האקספוננציאלית הבולטת בחלקה הראשון של המגיפה). חבל זה כולל אוכלוסייה בגודל דומה למדינת ישראל (10 מיליון תושבים), אך מספר המתים בו גבוה פי 50 (כ-15 אלף). כלומר אותו מודל מתנהג באופן שונה על פי אופי המדינה, תנאי ההתחלה והצעדים שננקטים לאורך הזמן.
רגע, אבל אם ככה אז איך נדע שהצעדים אינם מוגזמים או קלים מדי?
השאלה הזו היא כבר בממשק שבין המדענים המייצרים את המודל למדינאים המשתמשים בו. באופן בסיסי, טעויות הניבוי עלולות להיות או False positive (נזהה משהו כבעל משמעות כשלמעשה הוא אינו כזה) או False negative (נזהה משהו כחסר משמעות כשהוא בעצם נושא אותה). הרבה פעמים מתייחסים לשתי הטעויות באופן דומה אבל במציאות הדבר אינו כך.
אחד המאמרים המחכימים שהתפרסמו בעברית סביב משבר הקורונה נכתב על ידי מפכ״ל המשטרה האחרון רב-ניצב רוני אלשיך (״אובדן דרך בטיפול במגיפה״, 25.03.2020). אלשיך מעיד על עצמו כי איננו מדען, אך צבר ניסיון רב ב"ניהול מומחים" כלומר התמודדות עם תחזיות של מומחים בראי אי הוודאות.
הוא מסביר כי "ככלל, מקובל כי כאשר ישנה אי-ודאות, מייצרים 'התכווצות זמנית', מבצעים הערכת מצב הממוקדת בצמצום אי-הוודאות, ואז משחררים את חלקה ומתחילים לנהל סיכונים מבוקרים״. כלומר (1) יש משמעות מרכזית לסיכון, שעל פיו נקבע עד כמה לתת משקל להערכות מסוימות של המודל, ו-(2) משקל הסיכון צריך ללכת ולקטון עם הזמן. במונחים של מודל, מה שמציע אלשיך הוא בתחילת המשבר להעדיף טעות מסוג False positive (״ללכת על בטוח״, סך הכול מה שקורה באיטליה באמת מפחיד), ובהמשך לטייב את המודל (למשל על ידי דיוק בפרמטרים הנאספים, הוספת עוד פרמטרים חשובים והשמטת פרמטרים לא חשובים, שיפור הפעולות המתמטיות במודל; המצב בישראל, מסתבר, שונה מאוד ממה שבאיטליה) ובהתאם לנהל סיכונים ולאזן בין False positive ו- False negative.
אגב, גם לכך יש למתמטיקה פתרונות, למשל בדמות חישוב של ״פונקציית עלות״ שמתארת את ההשלכות של המשקלות השונים שניתן להצמיד לכל אחת מן הטעויות (או לסיכון ולסיכוי) על מנת להגיע לפתרון אופטימלי, אבל על כך בפעם אחרת. ספוילר: האם פונקציה זו חושבה נכונה בישראל? כנראה שלא.
אז איך מודל יכול לעזור לנו?
הכלי היעיל ביותר ברפואה, ובעולם בכלל, הוא הרטרוספקטוסקופ, או בעברית: מכשיר-לראייה-רטרוספקטיבית, או בפולנית: "אמרתי לך".
קל מאוד להיות חכם לאחר מעשה אבל בהקשר של וירוס הקורונה אין לנו הלוקסוס הזה ועל כן עלינו להשתמש בכל הכלים המדעיים והרפואיים שיש לנו, כולל במודלים. בעזרת מודלים אנחנו יכולים לשערך את מספר האנשים הנושאים את הוירוס בישראל (מדבקים או לא, סימפטומטיים או לא), הסיכוי לאישפוז או תמותה, איך המספרים הללו צפויים להשתנות עם הזמן, ואיך התערבויות שונות (כמו סגירת בתי ספר, חזרה לשבוע עבודה קצר, שינויים בתחבורה ציבורית, סגר כללי) צפויות להשפיע על התוצאות, בהתחשב במאפיינים המיוחדים של המדינה (למשל: מספר מיטות טיפול נמרץ) ושל המחלה (למשל: הפצה אפשרית בעיקר על ידי מפיצי-על, תחרות בין תת-זנים).
הערכות כאלו להשפעות של סוגים שונים של מדיניות נותנות בסיס למגוון רחב של שיקולים ומאפשרות לתכנן אסטרטגיה שתגן באופן מיטבי על בריאות הציבור מחד ותצמצם ככל האפשר השפעות שליליות לטווח קצר וארוך (כלכלה, בריאות נפשית וגופנית, חינוך). המודלים גם ממחישים לנו באופן מדוקדק עד כמה הקפדה על ריחוק חברתי והיגיינה הם משמעותיים, ובקרוב עם זרימת נתונים סרולוגיים יוכלו לספר לנו על חסינות האוכלוסיה ומשמעותה. שילוב נכון של הכלים והתהליכים שסקרנו (מודלים סטטיסטיים, מודלים מכניסטיים, שערוך פרמטרים נכון על סמך מאגרי מידע מהימנים, התחשבות בתנאי התחלה, הבררת מאפייני הבעיה, מדדי שגיאה, פונקציות עלות, כוונון מתמיד), יחד עם הבנות טובות של מומחים לתחום בעלי ניסיון מוכח בסיטואציות דומות והחלטות מושכלות ונטולות פניות של קובעי מדיניות יובילו להתמודדות מיטבית עם הנגיף והשלכותיו. כך, הזלזול במדע, בתחזיות רפואיות ובמודלים הובילו מדינות וקהילות מסוימות אל עברי פי פחת, בעוד שמדינות שמשתמשות במודלים בתבונה מראות תוצאות טובות יותר באופן משמעותי.
סיכום: בשבח המדע והרפואה
הפנדמיה הנוכחית החזירה לחזית הציבורית את המדע והרפואה, תחומי יסוד של התרבות והקיום האנושי מזה מאות שנים, שלעיתים נדחקות תחת אופנות מידיות, כוחניות וטוטאליות יותר כמו כספים, טכנולוגיה וריאליטי. בימים אלו, העולם נושא עיניו אל המדע והרפואה שיטפלו בו בחוליו, יובילו את צעדיו, ויפתחו עבורו בדיקות, תרופות וחיסונים.
על כן יש גם לשמר את האקלים התרבותי והמקצועי שהמדע והרפואה פועלים בהם. כי זהו האקלים שהוביל את המדע והרפואה להישגים האדירים שלהם, תאורטיים ויישומיים גם יחד, ורק מדע ורפואה במיטבם יצעידו אותנו אל מעבר למשבר הקורונה. ולבסוף, המדע מלמד אותנו על הנטייה האנושית הנהדרת להדחיק, לשכוח דברים שליליים ו״לעבור הלאה״. כל כך חשוב להשקיע במדע וברפואה הציבורית אף יותר גם ביום שאחרי. ושיבוא כבר.
פרופ' שחר ארזי, הפקולטה לרפואה, האונ׳ העברית; פרופ׳ בעז ברק וד"ר מור ניצן, הפקולטה למדעי הטבע, אונ׳ הרווארד; ד"ר יאני יובל, הפקולטה למדעי כדור הארץ, MIT; ד"ר נטע רביד, הפקולטה לתעשייה וניהול, הטכניון